
 ��ͼ����ֱ֪������ABCD���ڵ�ƽ�洹ֱ��ƽ��ABE����EAB=��ABC=90�㣬��DAB=60�㣬AB=AD=AE��PΪ�߶�BE���е㣮
��ͼ����ֱ֪������ABCD���ڵ�ƽ�洹ֱ��ƽ��ABE����EAB=��ABC=90�㣬��DAB=60�㣬AB=AD=AE��PΪ�߶�BE���е㣮���� ����ȡAE���е�F������DF��PF������֪֤��PF��DC����PF=DC�����ı���DCPFΪƽ���ı��Σ��ɵ�PC��DF����������ƽ�е��ж��ɵ�CP��ƽ��DAE��
��II���ɡ�BAE=90�㣬ƽ��ABCDƽ��ABE����ƽ��ABCD�ڹ�A��Az��AB���Ե�AΪԭ�㣬ֱ��AEΪx�ᣬֱ��ABΪy�ᣬAzΪz�Ὠ���ռ�ֱ������ϵA-xyz��
��AB=AD=AE=2�����E��C��D�����꣬��һ�����ƽ��ECD��ƽ��ƽ��ABC��һ�����������������������ɽǵ�����ֵ�ɵ�ƽ��CDE��ƽ��ABE���ɵ������Ǧȵ�����ֵ��
������Q��x��y��z������$\overrightarrow{EQ}=��\overrightarrow{EC}$��������������Q��2-2�ˣ�2�ˣ�$\sqrt{3}��$������P��1��1��0�����ɵ�$\overrightarrow{PQ}=��1-2�ˣ�2��-1��\sqrt{3}�ˣ�$�����ֱ��PQ��ƽ��CDE���ɵĽǵ�����ֵΪ$\frac{3\sqrt{6}}{14}$��ʽ���$��=\frac{2}{9}$��$��=\frac{2}{33}$��
��� ����֤����ȡAE���е�F������DF��PF��
��PΪBE�е㣬��PF��AB����PF=$\frac{1}{2}AB$��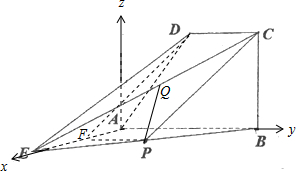
��ֱ������ABCD�У���DAB=60�㣬AB=AD��
�ɵ�DC��AB����DC=$\frac{1}{2}AB$��
��PF��DC����PF=DC�����ı���DCPFΪƽ���ı��Σ��ɵ�PC��DF��
��DF?ƽ��EAD��PC?ƽ��EAD����CP��ƽ��DAE��
��II���⣺�ߡ�BAE=90�㣬ƽ��ABCDƽ��ABE����ƽ��ABCD�ڹ�A��Az��AB��
���Ե�AΪԭ�㣬ֱ��AEΪx�ᣬֱ��ABΪy�ᣬAzΪz�Ὠ���ռ�ֱ������ϵA-xyz��
��AB=AD=AE=2������֪����E��2��0��0����C��0��2��$\sqrt{3}$����D��0��1��$\sqrt{3}$����
��$\overrightarrow{EC}=��-2��2��\sqrt{3}��$��$\overrightarrow{DC}=��0��1��0��$��
��ƽ��ECD�ķ�����Ϊ$\overrightarrow{n}$=��x��y��z����
��$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=-2x+2y+\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{DC}=y=0}\end{array}\right.$��ȡz=2����ƽ��ECD��һ��������Ϊ$\overrightarrow{n}$=��$\sqrt{3}$��0��2����
�֡�ƽ��ABC��һ��������Ϊ$\overrightarrow{m}$=��0��0��1����
��cos��=|cos��$\overrightarrow{m}��\overrightarrow{n}$��|=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{2}{\sqrt{7}}=\frac{2\sqrt{7}}{7}$��
��ƽ��CDE��ƽ��ABE���ɵ������Ǧȵ�����ֵΪ$\frac{2\sqrt{7}}{7}$��
���⣺�߶�EC�ϴ��ڵ�Q��ʹֱ��PQ��ƽ��CDE���ɵĽǵ�����ֵΪ$\frac{3\sqrt{6}}{14}$����ʱ$\frac{EQ}{EC}$=$\frac{2}{9}$��$\frac{EQ}{EC}$=$\frac{2}{33}$��
��Q��x��y��z������$\overrightarrow{EQ}=��\overrightarrow{EC}$����x-2��y��z��=��-2$�ˣ�2�ˣ�\sqrt{3��}$����
��$\left\{\begin{array}{l}{x-2=-2��}\\{y=2��}\\{z=\sqrt{3}��}\end{array}\right.$����Q��2-2�ˣ�2�ˣ�$\sqrt{3}��$����P��1��1��0����
��$\overrightarrow{PQ}=��1-2�ˣ�2��-1��\sqrt{3}�ˣ�$��
��ֱ��PQ��ƽ��CDE���ɵĽǵ�����ֵΪ$\frac{3\sqrt{6}}{14}$��
��|cos��$\overrightarrow{PQ}��\overrightarrow{n}$��|=|$\frac{\overrightarrow{PQ}•\overrightarrow{n}}{|\overrightarrow{PQ}||\overrightarrow{n}|}$|=$\frac{|\sqrt{3}��1-2�ˣ�+2\sqrt{3}��|}{\sqrt{2��1-2�ˣ�^{2}+3{��}^{2}}•\sqrt{7}}=\frac{3\sqrt{6}}{14}$��
��ã�$��=\frac{2}{9}$��$��=\frac{2}{33}$��
��$\frac{EQ}{EC}$=$\frac{2}{9}$��$\frac{EQ}{EC}$=$\frac{2}{33}$��
���� ���⿼������ƽ�е��ж�������ռ�����������˼ά������ѵ�������ÿռ������������������ǣ����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
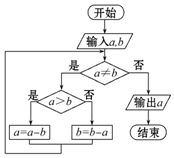 ijͬѧ���ݡ��������������Ƴ������ͼ��ͼ����������a��ֵΪ98��b��ֵΪ63����ִ�иó����ͼ����Ľ��Ϊ��������
ijͬѧ���ݡ��������������Ƴ������ͼ��ͼ����������a��ֵΪ98��b��ֵΪ63����ִ�иó����ͼ����Ľ��Ϊ��������| A�� | 0 | B�� | 7 | C�� | 14 | D�� | 21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ijСѧ�������ʴ���˶����ϣ���10��������10��Ů����һ���������Ĵ�������ͳ�ƣ��õ�������ʾ��Ҷͼ��
��ijСѧ�������ʴ���˶����ϣ���10��������10��Ů����һ���������Ĵ�������ͳ�ƣ��õ�������ʾ��Ҷͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| Ի�� | 8��1Ի | 8��7�� | 8��14�� | 8��18�� | 8��25�� |
| ƽ�����£��棩 | 33 | 30 | 32 | 30 | 25 |
| �õ�������ȣ� | 38 | 35 | 41 | 36 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{��}^{3}}{81}$+$\frac{1}{2}$ | B�� | $\frac{{��}^{3}}{81}$-$\frac{1}{2}$ | C�� | $\frac{2��}{3}$-$\frac{1}{2}$ | D�� | $\frac{2��}{3}$+$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com