
����Ŀ������ʡ����������������֮����֮�ƣ����ʳ����з�������ĸ��ʺ�������ʢ�������㣬�ǻ������ں��е�����Ϊ![]() ���������ں��еĺ������ĵ�λ��Ϊ
���������ں��еĺ������ĵ�λ��Ϊ![]() �����о������������
����������������![]() ��
��![]() �����ȣ����ⶨ����������ĺ�����Ϊ200��λʱ��������Ϊ
�����ȣ����ⶨ����������ĺ�����Ϊ200��λʱ��������Ϊ![]() .
.
��1����![]() ����
����![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ
��2�����㻨���㾲ֹʱ�������ĵ�λ��.
��3�����ij������������������1![]() ����ô���ĺ������ĵ�λ����ԭ���Ķ��ٱ���
����ô���ĺ������ĵ�λ����ԭ���Ķ��ٱ���
���𰸡���1��![]() ����2��
����2��![]() ����3��4��
����3��4��
��������
��1������������ģ����ʽ����![]() ��������֪�������
��������֪�������![]() ���ã�
���ã�
��2����![]() ���
���![]() ��
��
��3����![]() ���
���![]() ��
��![]() �Ĺ�ϵ���ɣ�
�Ĺ�ϵ���ɣ�
��1���������������![]() ��
��![]() �����ȣ�����
�����ȣ�����![]()
����Ϊ��![]() ʱ��
ʱ��![]() ������
������![]() �����
�����![]()
����![]()
��2���������㾲ֹʱ��![]() ����
����![]() ���
���![]()
��3���軨���㿪ʼ���ٶȼ�Ϊ![]() �������ĵ�λ��Ϊ
�������ĵ�λ��Ϊ![]() ���������ٶȼ�Ϊ
���������ٶȼ�Ϊ![]() �������ٺ�ĺ����ĵ�λ��Ϊ
�������ٺ�ĺ����ĵ�λ��Ϊ![]()
��Ϊ![]()
����Ϊ![]() ��
��![]()
����![]() �����������ĵ�λ����ԭ����4��.
�����������ĵ�λ����ԭ����4��.


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ������״������Ⱦ�ķ���������������Ͼ�.���ֵ��г�����һֱ�Ӹ߲���.Ϊ�˱��Ϸ������ʹ�Ӧ��Ϋ���Ŀ�����ҵ����������������������һ����ʱ�����ܵ����������ս��.Ϋ���з�����һ�ҿ���������ҵӵ��1000ƽ���ྻ���䣬�䱸�������ȵ��Զ���������5���������Ǹ�20����.�����鷢������������ҵ������Ӧ�������٣�����ÿ������һ�����IJ�������������5��ֻ����.�ִ������Ĵ��������г�ȡ��100ֻ��Ϊ���������һ������ָ��ֵ����������ָ��ֵ��������[20,40���ڵIJ�Ʒ��Ϊ�ϸ�Ʒ��������Ϊ���ϸ�Ʒ����ͼ��������Ƶ�ʷֲ�ֱ��ͼ.

��1����ͼ��ʵ��a��ֵ��
��2����ҵ�����ϸ�Ʒȫ�����ٺԺϸ�Ʒ���еȼ�ϸ�֣�����ָ��ֵ��������[25,30���ڵĶ�Ϊһ��Ʒ��ÿ���ۼ�2.4Ԫ������ָ��ֵ��������[20,25����[30,35���ڵĶ�Ϊ����Ʒ��ÿ���ۼ�Ϊ1.8Ԫ�������ĺϸ�Ʒ��Ϊ����Ʒ��ÿ���ۼ�Ϊ1.2Ԫ.
�ø���������һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е�Ƶ�ʴ�������в�Ʒ�г鵽һ����Ӧ�ȼ���Ʒ�ĸ���.����һ���˿��������2ֻ����֧���ķ���ΪX����λ��Ԫ��.��X�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������3����ͬ�ĺ���5����ͬ�İ���.
��1��ȫ��ȡ���ų�һ�У�3�������������������ŷ��ж����֣�
��2��������ȡ6������ĸ���������������ٵ�ȡ���ж����֣�
��3����ȡһ�������2�֣�ȡһ�������1�֣�������ȡ5����ʹ�ܷ�������7�ֵ�ȡ���ж����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ij�豸��ʹ������x���꣩����֧����ά����y��Ԫ�����µ�ͳ�����ϣ�
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
��1������ɢ��ͼ���ж��Ƿ�������أ�
��2�����������أ������Իع鷽�̣�
��3������ʹ������Ϊ10��ʱ��ά�����Ƕ��٣�
��ע���ٲο���ʽ���ع鷽��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ��
��
�ڲο����ݣ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰn���
��ǰn���![]() ��
�� ![]() �ǵȲ����У���
�ǵȲ����У���![]() .
.
������������![]() ��ͨ�ʽ��
��ͨ�ʽ��
�������� .������
.������![]() ��ǰn���
��ǰn���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ�˽���Ͷ������������Ӱ�죬�����ɵ�����Ͷ��4��Ԫ�����ã��������ص�����������Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������ڹ�����Ա����ʧ��������ݶ�ʧ��������ȷ�������Ǵ�0��ʼ������.
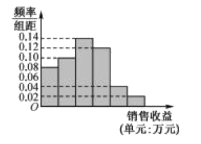
��1������Ƶ�ʷֲ�ֱ��ͼ����ͼ�и�С�����εĿ��ȣ�
��2���Թ��Ƹù�˾�����ɵ�����Ͷ��4��Ԫ������֮��Ӧ���������ƽ��ֵ���Ը���������е�ֵ���������ȡֵ����
��3���ù�˾�������Ƶ��о��������������һЩ���ݣ��������õ��±���
���Ͷ�� | 1 | 2 | 3 | 4 | 5 |
�������� | 2 | 3 | 3 | 7 |
�ɱ��е�������ʾ��![]() ��
��![]() ֮�������������ع�ϵ���뽫��2���Ľ������հ����������
֮�������������ع�ϵ���뽫��2���Ľ������հ����������![]() ����
����![]() �Ļع�ֱ�߷���.���ο���ʽ��
�Ļع�ֱ�߷���.���ο���ʽ��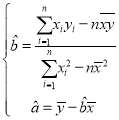 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����R�ϵ�ż�������ҵ�x��0ʱ��f��x����x2��2x��
��1����f��0����f��f��1������ֵ��
��2������f��x���Ľ���ʽ��
��3��������x�ķ���f��x����m��0���ĸ���ͬ��ʵ���⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ҹ������з��ij���ϵ�л����ƵƵ����ɹ�����־���ҹ��ڸ��������ﵽ����һ��ˮƽ.����ƽ���������Ϊ![]() ��ȥ���ƽ�����Ļ����Ч�غ�����Ϊ
��ȥ���ƽ�����Ļ����Ч�غ�����Ϊ![]() ������ķ����ٶ�Ϊ
������ķ����ٶ�Ϊ![]() ����ʼ�ٶ�Ϊ
����ʼ�ٶ�Ϊ![]() ����֪���ϵʽΪ��¶��Ʒ�˹����ʽ��
����֪���ϵʽΪ��¶��Ʒ�˹����ʽ��![]() ������
������![]() �ǻ��������������Ի�����ٶȣ�����
�ǻ��������������Ի�����ٶȣ�����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() Ϊ����Ȼ������
Ϊ����Ȼ������![]() ��
��![]() .
.
��1�����ϣ����������ٶ�![]() �ֱ�ﵽ��һ�����ٶ�
�ֱ�ﵽ��һ�����ٶ�![]() ���ڶ������ٶ�
���ڶ������ٶ�![]() �����������ٶ�
�����������ٶ�![]() ʱ����
ʱ����![]() ��ֵ����ȷ��С�������1λ��.
��ֵ����ȷ��С�������1λ��.
��2�����ϣ��![]() �ﵽ
�ﵽ![]() �����������������ֵΪ
�����������������ֵΪ![]() ������
������![]() ����СֵΪ���٣���ȷ��С�������1λ�����ɴ�ָ����ʵ������.
����СֵΪ���٣���ȷ��С�������1λ�����ɴ�ָ����ʵ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() Ϊֱ�����Σ�
Ϊֱ�����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
��1����֤:![]() ��ƽ��
��ƽ��![]() ��
��
��2������![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com