
 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)分析 (1)以点D为坐标原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系.利用cos$<\overrightarrow{DB},\overrightarrow{EF}>$=$\frac{\overrightarrow{DB}•\overrightarrow{EF}}{|\overrightarrow{DB}||\overrightarrow{EF}|}$,即可得出.
(2)$G(\frac{1}{2},0,0)$,设平面$\overrightarrow{BEF}$的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BF}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{GF}=0}\end{array}\right.$,可得平面GBF的法向量$\overrightarrow{{n}_{1}}$=(4,-2,1),同理可得平面BEF的法向量$\overrightarrow{n_1}=(1,1,1)$.利用cos$<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$,即可得出.
(3)连接AE,取中点为O,连接OA,OB,OC,OD,OE,由已知易得OA=OB=OC=OD=OE,可得DO长为所求球的半径.
解答 解:(1)以点D为坐标原点,分别以DA,DC,DF所在直线为x轴,y轴,z轴建立空间直角坐标系.
D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),E(0,1,1),F(0,0,2).
$\overrightarrow{DB}$=(1,1,0),$\overrightarrow{EF}$=(0,-1,1),cos$<\overrightarrow{DB},\overrightarrow{EF}>$=$\frac{\overrightarrow{DB}•\overrightarrow{EF}}{|\overrightarrow{DB}||\overrightarrow{EF}|}$=$\frac{1}{2}$,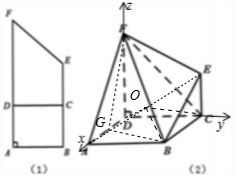
∴异面直线BD与EF所成角为$\frac{π}{3}$.
(2)$G(\frac{1}{2},0,0)$,
设平面$\overrightarrow{BEF}$的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),
$\overrightarrow{BF}$=(1,1,-2),$\overrightarrow{GF}$=$(-\frac{1}{2},0,2)$.
∴$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BF}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{GF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{x+y-2z=0}\\{-\frac{1}{2}x+2z=0}\end{array}\right.$,
取平面GBF的法向量$\overrightarrow{{n}_{1}}$=(4,-2,1),
同理可得平面BEF的法向量$\overrightarrow{n_1}=(1,1,1)$.
cos$<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{7}}{7}$.
∵二面角G-BF-C与两向量的夹角互补,
∴二面角G-BF-C的余弦值为:$-\frac{{\sqrt{7}}}{7}$.
(3)连接AE,取中点为O,连接OA,OB,OC,OD,OE,
由已知易得OA=OB=OC=OD=OE,∴DO长为所求球的半径.
O$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,$\overrightarrow{DO}$=$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,∴r=$|\overrightarrow{DO}|$=$\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$.
∴S球的表面积=4πr2=3π.
点评 本题考查了空间位置关系、空间角、法向量的应用、向量夹角公式、球的表面积、直角三角形的性质,考查了推理能力与计算能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 100° | B. | 160° | C. | 100°或160° | D. | 130° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{2}{3},+∞})$ | B. | $({\frac{2}{3},+∞})$ | C. | $[{-\frac{1}{12},+∞})$ | D. | $({-\frac{1}{12},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若长方体的长、宽、高各不相同,则长方体的三视图中不可能有正方形(以长×宽所在的平面为主视面) | |
| B. | 照片是三视图中的一种 | |
| C. | 若三视图中有圆,则原几何体中一定有球体 | |
| D. | 圆锥的三视图都是等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=3 | B. | y=$\sqrt{1-{x}^{2}}$ | C. | x2+2xy=1(x≠±1) | D. | x2+y2=9(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com