
分析 (1)化简f(x)≤0,构造函数令$g(x)=\frac{lnx+1}{x}$,通过函数的导数,判断函数的单调性,求出最值,即可得到结果.
(2)对任意的x∈[1,+∞),函数g(x)≥0恒成立,求出函数的导数,令h(x)=g′(x),再求解函数的导数,通过10当a≤0,20当$a≥\frac{1}{3}$,30a∈(0,$\frac{1}{3}$),分别请假函数的最值,利用恒成立,请假即可.
解答 解:(1)$f(x)≤0⇒p≥\frac{lnx+1}{x}$,
令$g(x)=\frac{lnx+1}{x}$,则${g^'}(x)=\frac{-lnx}{x^2}$,
∴x∈(0,1),g(x)↑,x∈(1,+∞),g(x)↓,
∴g(x)max=g(1)=1,
∴p≥1.
(2)g′(x)=3ax-lnx-3a,
令h(x)=g′(x),
则${h^'}(x)=\frac{3ax-1}{x}$,g(1)=0,g′(1)=0,
10当a≤0,x∈[1,+∞),h′(x)≤0⇒h(x)↓
又h(1)=g′(1)=0⇒g′(x)=h(x)≤0⇒g(x)↓⇒g(x)≤0(x∈[1,+∞)),
不符合题意,舍,
20当$a≥\frac{1}{3}$,x∈[1,+∞),h′(x)≥0⇒h(x)↑
又h(1)=g′(1)=0⇒g′(x)=h(x)≥0⇒g(x)↑⇒g(x)≥0(x∈[1,+∞)),
30a$∈(0,\frac{1}{3})$,x∈[1,+∞),${h^'}(x)=0⇒x=\frac{1}{3a}>1$$⇒x∈(1,\frac{1}{3a})$时h′(x)<0,
∴$x∈(1,\frac{1}{3a})$时,g′(x)=h(x)↓,又g(1)=0,
∴$x∈(1,\frac{1}{3a}]$时,g(x)≤0
(必须证明,如果只证明$a≥\frac{1}{3}$符合题意,没有证明另外情况不符合题意的减3到5分)
点评 本题考查函数的导数的综合应用,函数的最值以及函数的单调性的应用,考查分类讨论思想以及转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{x+1}{x+2}$ | B. | f(x)=$\frac{x}{x+1}$ | C. | f(x)=$\frac{x-1}{x}$ | D. | f(x)=$\frac{1}{x+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C为BE的中点,AD=1,如图(1),沿直线CD折成直二面角,连结部分线段后围成一个空间几何体(如图2)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3$\sqrt{2}$) | B. | (3$\sqrt{2}$,+∞) | C. | (-∞,3$\sqrt{2}$) | D. | (0,$\sqrt{2}$)∪(3$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
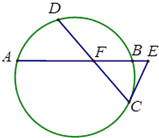 如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )
如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
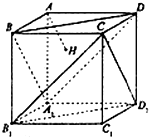 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com