
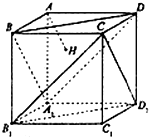
 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)分析 首先,判断三棱锥 A-BA1D为正三棱锥,然后,得到△BA1D为正三角形,得到H为A在平面A1BD内的射影,然后,根据平面A1BD与平面B1CD1平行,得到选项B正确,最后,结合线面角和对称性求解
解答 解:∵AB=AA1=AD,
BA1=BD=A1D,
∴三棱锥 A-BA1D为正三棱锥,
∴点H是△A1BD的垂心;
故①为真命题;
∵平面A1BD与平面B1CD1平行,
∵AH⊥平面A1BD,
∵平面A1BD⊥平面BC1D,
∴AH垂直平面CB1D1,
故②为真命题;
根据正方体的对称性得到
AH的延长线经过C1,
故③为真命题
对于选项C,
∵AA1∥BB1,
∴∠A1AH就是直线AH和BB1所成角,
在直角三角形AHA1中,
∵AA1=1,A1H=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$×$\sqrt{2}$=$\frac{\sqrt{6}}{3}$,
∴sin∠A1AH=$\frac{\sqrt{6}}{3}$,
故④为假命题;
AH与底面A1B1C1D1所成的角θ满足sinθ=$\frac{\sqrt{3}}{3}$,
∴θ=arcsin$\frac{\sqrt{3}}{3}$,
由AH垂直平面A1BD,
可得平面A1BD与底面A1B1C1D1所成的角为90°-arcsin$\frac{\sqrt{3}}{3}$≠60°.
故⑤为假命题;
故答案为:①②③.
点评 本题以命题的真假判断与应用为载体,考查了正方体的几何特征,线面垂直,直线与平面的夹角,二面角等知识点,难度中档.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪[1,+∞) | B. | [-1,0] | C. | [0,1] | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3≤x≤1且x≠-2} | B. | $\{x|x≤-1或x≥\frac{1}{3}\}$ | C. | {x|-1≤x≤3且x≠0} | D. | $\{x|-1≤x≤\frac{1}{3}且x≠0\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com