
| A. | (-∞,-1]∪[1,+∞) | B. | [-1,0] | C. | [0,1] | D. | [-1,1] |
分析 利用偶函数的性质将不等式等价转化,由基本初等函数和复合函数的单调性,判断出f(x)在(-∞,0]上单调性,由偶函数的性质判断出在[0,+∞)上的单调性,由单调性列出不等式,求出a的取值范围.
解答 解:∵函数f(x)是定义在R上的偶函数,
∴不等式f(a)+f(-a)≤2f(1)等价为2f(a)≤2f(1),
即f(a)≤f(1),
∴等价为f(|a|)≤f(1),
∵当x≤0时,f(x)=ex-$\frac{1}{x-1}$,
∴f(x)在区间(-∞,0]上单调递增,
∴偶函数f(x)在区间[0,+∞)上单调递减,
∴|a|≥1,即a≤-1或a≥1,
则实数a取值范围是(-∞,-1]∪[1,+∞),
故选:A.
点评 本题考查了函数的奇偶性和单调性,基本初等函数的单调性,利用函数奇偶性的性质、单调性将不等式等价转化是解题的关键,考查了函数思想、转化思想.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
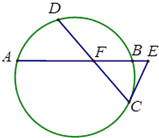 如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )
如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
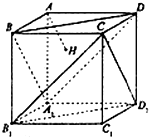 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com