
分析 (Ⅰ)设{an}的首项为a1,公差为d,代入求得an=n.
(Ⅱ)先求得${S}_{n}=\frac{n(n+1)}{2}$,代入求得${b}_{n}=\frac{2}{n(n+1)}$.
(Ⅲ)由${b}_{n}=2(\frac{1}{n}-\frac{1}{n+1})$,利用裂项求和求得${b}_{1}+{b}_{2}+…+{b}_{n}=2-\frac{2}{n+1}<2$.
解答 解:(Ⅰ)设{an}的首项为a1,公差为d,
∵等差数列{an}的前n项之和为Sn,${b}_{n}=\frac{1}{{S}_{n}}$,且${a}_{3}{b}_{3}=\frac{1}{2}$,S3+S5=21.
∴$\left\{\begin{array}{l}({a}_{1}+2d)×\frac{1}{3{a}_{1}+\frac{3×2}{2}d}=\frac{1}{2}\\ 3{a}_{1}+\frac{3×2}{2}d+5{a}_{1}+\frac{5×4}{2}d=21\end{array}\right.$,
解得a1=1,d=1,∴an=n.
(Ⅱ)∵a1=1,d=1,∴
Sn=n+$\frac{n(n-1)}{2}×1$=$\frac{n(n+1)}{2}$,
∵${S}_{n}=\frac{n(n+1)}{2}$,${b}_{n}=\frac{1}{{S}_{n}}$,
∴${b}_{n}=\frac{2}{n(n+1)}$.
证明:(Ⅲ)∵${b}_{n}=2(\frac{1}{n}-\frac{1}{n+1})$,
∴b1+b2+…+bn=$2[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})]$=$2-\frac{2}{n+1}$<2.
点评 本题考查数列的通项公式的求法,考查数列的前n项和小于2的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,3$\sqrt{2}$) | B. | (3$\sqrt{2}$,+∞) | C. | (-∞,3$\sqrt{2}$) | D. | (0,$\sqrt{2}$)∪(3$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
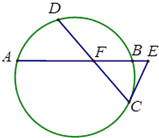 如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )
如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=$\sqrt{2}$,AF=2BF,若CE与圆相切,且CE=$\frac{\sqrt{7}}{2}$,则BE的长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要非充分条件 | B. | 充分非必要条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
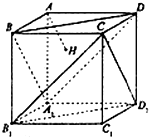 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )
用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )| A. | 120 | B. | 150 | C. | 180 | D. | 240 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com