
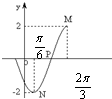
分析 根据三角函数的图象与性质,得出A、T、ω与φ的值,即可写出函数f(x)的解析式.
解答 解:由题意可知A=2,
T=2($\frac{2π}{3}$-$\frac{π}{6}$)=π,
∴ω=$\frac{2π}{T}$=2;
又当x=$\frac{π}{6}$时f(x)=-2,
∴2sin(2×$\frac{π}{6}$+φ)=-2,
∴sin($\frac{π}{3}$+φ)=-1,
∴$\frac{π}{3}$+φ=2kπ-$\frac{π}{2}$,k∈Z;
又φ∈(-π,π),
∴φ=-$\frac{5π}{6}$,
∴函数f(x)的解析式为f(x)=2sin(2x-$\frac{5π}{6}$).
故答案为:f(x)=2sin(2x-$\frac{5π}{6}$).
点评 本题主要考查了根据函数y=Asin(ωx+φ)的部分图象求解析式的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
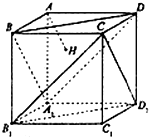 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,真命题的编号是①②③(写出所有真命题的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )
用5种不同颜色给图中的4个区域涂色,每个区域涂1种颜色,相邻区域不能同色,求不同的涂色方法共有多少种( )| A. | 120 | B. | 150 | C. | 180 | D. | 240 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
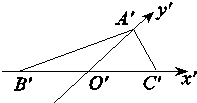 已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )
已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=$\frac{\sqrt{3}}{2}$,那么原△ABC中∠ABC的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com