
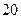 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为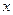 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当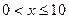 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当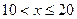 时,相邻两车之间保持
时,相邻两车之间保持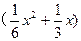 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 . (I)将
. (I)将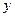 表示为
表示为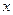 的
的 函数;(II)求车队通过隧道时间
函数;(II)求车队通过隧道时间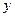 的最小值及此时车队的速度.
的最小值及此时车队的速度.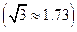
科目:高中数学 来源:不详 题型:解答题
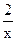 的值域为[3,9],K
的值域为[3,9],K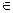 [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.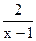 的值域为[7,11],K
的值域为[7,11],K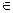 [7,11]时,g(x)=K
[7,11]时,g(x)=K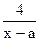 -b , x>a
-b , x>a查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
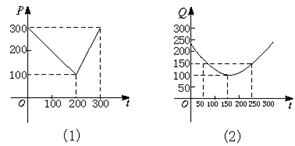
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com