
设不等式 的解集为M.
的解集为M.
(1)如果 ,求实数
,求实数 的取值范围;
的取值范围;
(2)如果 ,求实数
,求实数 的取值范围.
的取值范围.
(1)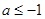 或
或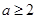 ;(2)
;(2)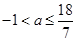 .
.
解析试题分析:本题考查含参一元二次不等式的解法及二次函数图像的性质等基础知识,考查转化思想、分类讨论思想等数学思想方法.第一问,由于抛物线开口向上,要使不等式的解集不为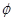 ,只需
,只需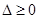 ;第二问,一元二次不等式含参数
;第二问,一元二次不等式含参数 ,对应的一元二次方程是否有解取决于
,对应的一元二次方程是否有解取决于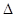 ,所以本问讨论
,所以本问讨论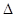 的三种情况,在每一种情况下,求出方程的根,写出不等式的解集,利用子集关系列出不等式,求
的三种情况,在每一种情况下,求出方程的根,写出不等式的解集,利用子集关系列出不等式,求 的取值范围.
的取值范围.
试题解析:(1)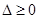 ,
,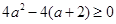 ,∴
,∴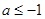 或
或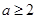 . 4分
. 4分
(2)①当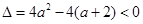 ,即
,即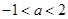 时,
时,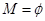 ,满足题意; 6分
,满足题意; 6分
②当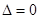 时,
时,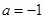 或
或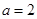 ,
,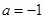 时,
时,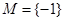 ,不合题意;
,不合题意;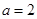 时,
时,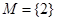 ,满足题意; 8分
,满足题意; 8分
③当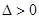 ,即
,即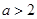 或
或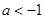 时,令
时,令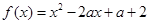 ,要使
,要使 ,只需
,只需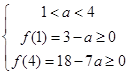 , 10分
, 10分
得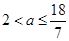 ,综上,
,综上,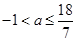 . 12分
. 12分
考点:1.二次函数的判别式;2.含参一元二次不等式的解法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
如图是某重点中学学校运动场平面图,运动场总面积15000平方米,运动场是由一个矩形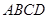 和分别以
和分别以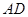 、
、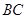 为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,
为直径的两个半圆组成,塑胶跑道宽8米,已知塑胶跑道每平方米造价为150元,其它部分造价每平方米80元,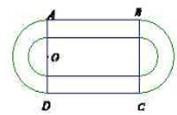
(Ⅰ)设半圆的半径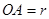 (米),写出塑胶跑道面积
(米),写出塑胶跑道面积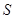 与
与 的函数关系式
的函数关系式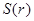 ;
;
(Ⅱ)由于受运动场两侧看台限制, 的范围为
的范围为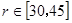 ,问当
,问当 为何值时,运动场造价最低(第2问
为何值时,运动场造价最低(第2问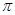 取3近似计算).
取3近似计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,且不等式
,且不等式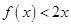 的解集为
的解集为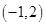 .
.
(1)方程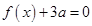 有两个相等的实根,求
有两个相等的实根,求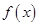 的解析式;
的解析式;
(2)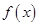 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数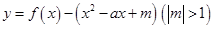 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与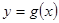 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com