
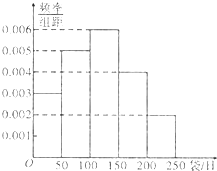
 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.分析 (Ⅰ)估计平均值为取各个小矩形中点数据求得.
(Ⅱ)不低于100袋的概率为0.6,低于50袋的概率为0.15,设事件A表示有两天日销售量不低于100袋且另一天销售量低于50袋,求得概率.
(Ⅲ)不低于150袋的概率为0.3.满足二项分布,利用二项分布求得分布列
解答 解析:(Ⅰ)估计平均值为25×0.15+75×0.25+125×0.3+175×0.2+225×0.1=117.5.(3分)
(Ⅱ)不低于100袋的概率为0.6,低于50袋的概率为0.15,设事件A表示有两天日销售量不低于100袋且另一天销售量低于50袋,则P(A)=C${\;}_{3}^{2}$(0.6)2×0.15=0.162.(6分)
(Ⅲ)不低于150袋的概率为0.3,X~B(3,0.3),
P(X=0)=C${\;}_{3}^{0}$(0.7)3=0.343,P(X=1)=C${\;}_{3}^{1}$(0.7)2×0.3=0.441,
P(X=2)=C${\;}_{3}^{2}$×0.7×0.32=0.189,P(X=3)=C${\;}_{3}^{3}$×0.33=0.027.
X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评 本题主要考查频率分布直方图和二项分布,属于中档题目,高考常有涉及


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).
已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
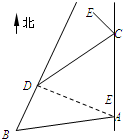 如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com