
分析 根据新定义,[x]表示不超过x的最大整数,{x}=x-[x],需要分类讨论,根据条件得到x=a+$\frac{1}{a(a+1)}$,继而求出a的可能值,最后代入计算即可.
解答 解:显然,x不可能是整数,否则由于{x}=0,方程[x]•{x}•],x=1不可能成立.设[x]=a,
则{x}=x-a,x=a+1,代入得a(x-a)(a+1)=1,解得x=a+$\frac{1}{a(a+1)}$.
考虑到x∈[0,6],且[x]≠0,所以a=1,2,3,4,5,故符合条件的解有5个,即m=5,
则x1+x2+…+xm=x1+x2+…+x5=$\frac{5(5+1)}{2}$+1-$\frac{1}{5+1}$=$\frac{95}{6}$,
故答案为:$\frac{95}{6}$.
点评 本题考查了函数的值,需要分类进行讨论,新定义一般需要认真读题,理解题意,灵活利用已知定义,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
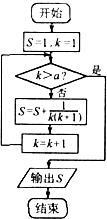
| A. | $\frac{6}{7}$ | B. | $\frac{15}{8}$ | C. | $\frac{13}{7}$ | D. | $\frac{11}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
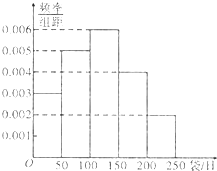 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com