
分析 将一颗骰子先后抛掷2次,含有36个等可能基本事件,两数中至少有一个奇数包含两个数有一个奇数,两个数都是奇数两种情况,这样做起来比较繁琐,可以选用它的对立事件来,对立事件是两数均为偶数,通过列举得到结论.
解答 解:将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
记“两数中至少有一个奇数”为事件A,
则事件A与“两数均为偶数”为对立事件,
两数都是偶数包含(2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6)共9中结果,
∴P(A)=1-$\frac{9}{36}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$
点评 本题考查的是古典概型,学好古典概型可以为其它概率的学习奠定基础,同时有利于理解概率的概念,有利于计算一些事件的概率,有利于解释生活中的一些问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | b1<a1<a2<b2<b3<a3 | B. | a1<b1<b2<a2<a3<b3 | ||
| C. | a1<a2<b1<b2<a3<b3 | D. | b1<b2<a1<a2<b3<a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
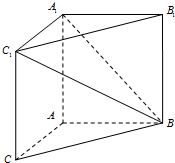 如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,
如图,在三棱柱ABC-A1B1C1中,AB=3,AA1=AC=4,AA1⊥平面ABC; AB⊥AC,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).
已知:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,短半轴长为$\sqrt{3}$;斜率为$\frac{b}{a}$的动直线l与椭圆C交于A,B两点,与x轴,y轴相交于P,Q两点(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com