
分析 (1)对函数求导,令导函数为0,得导函数的根,做表,通过导函数的正负确定原函数的增减.
(2)将所要证明的式子变形,建立一个函数,求导后再建立一个新的函数,再求导.需要用到两次求导.再来通过最值确定正负号,再来确实原函数的单调性.
解答 解:(1)f(x)的定义域为(0,+∞),
a=2时,f(x)=lnx+$\frac{e}{x}$
f′(x)=$\frac{1}{x}$-$\frac{e}{{x}^{2}}$=$\frac{x-e}{{x}^{2}}$
令f′(x)=0,得x=e
①当0<x<e时,f′(x)<0,则f(x)在区间(0,e)上是单调递减的
②当e<x时,f′(x)>0,则f(x)在区间(e,+∞)上是单调递增的
∴f(x)的递减区间是(0,e),单增区间是(e,+∞).
(2)原式等价于xlnx+a+e-2-ax≥0在(0,+∞)上恒成立.
令g(x)=xlnx+a+e-2-ax.
∵g′(x)=lnx+1-a
令g′(x)=0,得x=ea-1
①0<x<ea-1时,g′(x)<0,g(x)单调递减
②ea-1<x时,g′(x)>0,g(x)单调递增
∴g(x)的最小值为g(ea-1)=(a-1)ea-1+a+e-2-aea-1=a+e-2-ea-1.
令t(x)=x+e-2-ea-1.∵t′(x)=1-ea-1.
令t′(x)=0.得x=1.且
③0<x<1时,t′(x)>0,t(x)单调递增
④1<x时,t′(x)<0,t(x)单调递减
∴当a∈(0,1)时,g(x)的最小值t(a)>t(0)=e-2-$\frac{1}{e}$=$\frac{e(e-2)-1}{e}$>0.
当a∈[1,+∞)时,g(x)的最小值为t(a)=a+e-2-ea-1≥0=t(2).
∴a∈[1,2].
综上得:a∈(0,2].
点评 本题主要考查函数求导来寻找单调区间及极值和最值.尤其是第二问需要对函数求导后再建立一个新的函数求导,这也是一个常见类型.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(2sin2)>f(3sin3)>f(4sin4) | B. | f(4sin4)>f(3sin3)>f(2sin2) | ||
| C. | f(3sin3)>f(4sin4)>f(2sin2) | D. | f(2sin2)>f(4sin4)>f(3sin3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
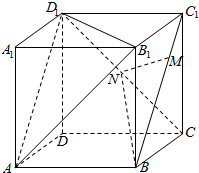 如图,正方体ABCD-A1B1C1D1中,N为CD1中点,M为线段BC1上的动点(M不与B,C1重合),以下四个命题:
如图,正方体ABCD-A1B1C1D1中,N为CD1中点,M为线段BC1上的动点(M不与B,C1重合),以下四个命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
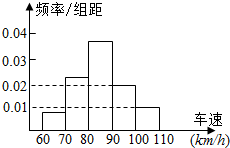 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )| A. | 12辆 | B. | 80辆 | C. | 100辆 | D. | 120辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间x | 3 | 5 | 7 |
| 价格f(x) | 13 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com