
���� ��1��������Բ�������ʹ�ʽ�͵�������Բ���̣��ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��2�����ۢٵ�k������ʱ���ڵ�k����ʱ����ֱ��Ϊy=kx+m��A��x1��y1����B��x2��y2������ֱ��y=kx+m������Բ���̣�����Τ�ﶨ�����ҳ���ʽ���Լ�ֱ�ߺ�Բ���е�������d=r����ϻ�������ʽ���ɵõ�������������ֵ��ֱ��l�ķ��̣�
��� 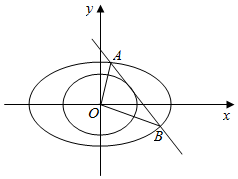 �⣺��1��������ɵã�e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$��a2-b2=c2��
�⣺��1��������ɵã�e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$��a2-b2=c2��
�㣨1��$\frac{\sqrt{6}}{3}$��������Բ���̣��ɵ�$\frac{1}{{a}^{2}}$+$\frac{2}{3{b}^{2}}$=1��
���a=$\sqrt{3}$��b=1��
������Բ�ķ���Ϊ$\frac{{x}^{2}}{3}$+y2=1��
��2���ٵ�k������ʱ��x=��$\frac{\sqrt{3}}{2}$ʱ���ɵ�y=��$\frac{\sqrt{3}}{2}$��
S��OAB=$\frac{1}{2}$��$\sqrt{3}$��$\frac{\sqrt{3}}{2}$=$\frac{3}{4}$��
�ڵ�k����ʱ����ֱ��Ϊy=kx+m��A��x1��y1����B��x2��y2����
��ֱ��y=kx+m������Բ���̿ɵã�1+3k2��x2+6kmx+3m2-3=0��
x1+x2=-$\frac{6km}{1+3{k}^{2}}$��x1x2=$\frac{3{m}^{2}-3}{1+3{k}^{2}}$��
��ֱ��l��ԲO��x2+y2=$\frac{3}{4}$���У��ɵ�$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{3}}{2}$��
����4m2=3��1+k2����
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{��\frac{-6km}{1+3{k}^{2}}��^{2}-\frac{12��{m}^{2}-1��}{1+3{k}^{2}}}$
=$\sqrt{3}$•$\sqrt{\frac{1+10{k}^{2}+9{k}^{4}}{1+6{k}^{2}+9{k}^{4}}}$=$\sqrt{3}$•$\sqrt{1+\frac{4{k}^{2}}{1+6{k}^{2}+9{k}^{4}}}$
=$\sqrt{3}$•$\sqrt{1+\frac{4}{9{k}^{2}+\frac{1}{{k}^{2}}+6}}$��$\sqrt{3}$•$\sqrt{1+\frac{4}{2\sqrt{9}+6}}$=2��
���ҽ���9k2=$\frac{1}{{k}^{2}}$ ��k=��$\frac{\sqrt{3}}{3}$ʱ�Ⱥų�����
�ɵ�S��OAB=$\frac{1}{2}$|AB|•r��$\frac{1}{2}$��2��$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$��
���С�OAB��������ֵΪ$\frac{\sqrt{3}}{2}$����ʱֱ�߷���y=��$\frac{\sqrt{3}}{3}$x��1��
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ�͵�������Բ���̣����������ε���������ֵ��ע�����÷������۵�˼�뷽��������ֱ�߷��̺���Բ���̣�����Τ�ﶨ�����ҳ���ʽ���Լ�ֱ�ߺ�Բ���е�������d=r���ͻ�������ʽ�����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1]��[3��+�ޣ� | B�� | [1��3] | C�� | ��3��+�ޣ� | D�� | ��-�ޣ�-1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{6}$ | D�� | $\frac{��}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | -7 | C�� | 7 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
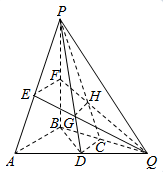 ��ͼ��ʾ��������P-ABQ�У�PB��ƽ��ABQ��BA=BP=BQ��D��C��E��F�ֱ���AQ��BQ��AP��BP���е㣬AQ=2BD��PD��EQ���ڵ�G��PC��FQ���ڵ�H������GH��
��ͼ��ʾ��������P-ABQ�У�PB��ƽ��ABQ��BA=BP=BQ��D��C��E��F�ֱ���AQ��BQ��AP��BP���е㣬AQ=2BD��PD��EQ���ڵ�G��PC��FQ���ڵ�H������GH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
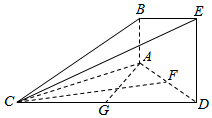 ��ͼ����֪AB��ƽ��ACD��DE��ƽ��ACD����ACD�ǵȱ������Σ�AD=DE=2AB=2��F��G�ֱ�ΪAD��DC���е㣮
��ͼ����֪AB��ƽ��ACD��DE��ƽ��ACD����ACD�ǵȱ������Σ�AD=DE=2AB=2��F��G�ֱ�ΪAD��DC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���x���֣�����Ӧ�������ܺ�y���ֱ�ú���ļ����������
����ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���x���֣�����Ӧ�������ܺ�y���ֱ�ú���ļ����������| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Vp��q | B�� | �Vp�ĩVq | C�� | p�ĩVq | D�� | p��q |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com