
分析 原式分母看做“1”,利用同角三角函数间的基本关系化简.
解答 解:(1)$\sqrt{1-si{n}^{2}100°}$=$\sqrt{1-si{n}^{2}80}$=cos80,
(2)$\frac{sinα+cosα}{2sinα-cosα}$=$\frac{tanα+1}{2tanα-1}$,
sin2α+sinαcosα+3cos2α=$\frac{si{n}^{2}α+sinαcosα+3co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{ta{n}^{2}α+tanα+3}{1+ta{n}^{2}α}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
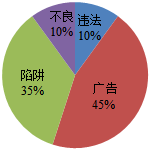 2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.
2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.| 条数 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) |
| 人数 | 1 | 2 | 5 | 9 | 5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com