
分析 (1)利用诱导公式化简已知条件,求出角的正弦函数与余弦函数值,即可求解.
(2)利用诱导公式化简所求的表达式,利用已知条件代入求解即可.
解答 解:(1)tan(π-α)=-$\frac{1}{2}$,
可得tanα=$\frac{1}{2}$,α为第三象限角,cosα=2sinα,sin2α+cos2α=1,
解得sinα=-$\frac{\sqrt{5}}{5}$.
cos($\frac{π}{2}$+α)=-sinα=-$\frac{\sqrt{5}}{5}$;
(2)$\frac{2sin(π-α)-3cos(π+α)}{3cos(π-α)+4sin(-α)}$
=$-\frac{2sinα+3cosα}{3cosα+4sinα}$
=$-\frac{2sinα+6sinα}{6sinα+4sinα}$
=-$\frac{4}{5}$.
点评 本题考查诱导公式以及同角三角函数的基本关系式的应用,考查计算能力.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | [-1,3] | C. | (-∞,3] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:填空题
如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:
①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;
④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.
其中正确的是 (写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源:2017届河南新乡一中高三9月月考数学(文)试卷(解析版) 题型:解答题
如图,四棱锥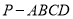 中,底面
中,底面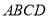 为矩形,
为矩形,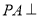 平面
平面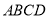 ,
,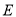 是
是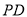 的中点.
的中点.

(1)证明: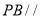 平面
平面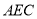 ;
;
(2)设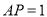 ,
,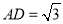 ,三棱锥
,三棱锥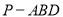 的体积
的体积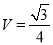 ,求
,求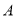 到平面
到平面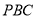 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com