
分析 a=bcos(A+B)=-bcosC,可得sinA=-sinBcosC,C为钝角,化为tanC=-2tanB.由上面可得:A,B为锐角,tanB>0,tanA>0.可得tanA=-tan(B+C)=$\frac{tanB}{1+2ta{n}^{2}B}$,利用基本不等式的性质即可得出tanA的范围.tan(A+$\frac{π}{4}$)=$\frac{2}{1-tanA}$-1,即可得出最大值.
解答 解:∵a=bcos(A+B)=-bcosC,
∴sinA=-sinBcosC,C为钝角.
∴sin(B+C)+sinBcosC=0,
化为tanC=-2tanB.
由上面可得:A,B为锐角,tanB>0,tanA>0.
∴tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$=$\frac{tanB}{1+2ta{n}^{2}B}$=$\frac{1}{\frac{1}{tanB}+2tanB}$≤$\frac{1}{2\sqrt{2}}$,当且仅当tanB=$\frac{\sqrt{2}}{2}$时取等号.
1-tanA≥$1-\frac{1}{2\sqrt{2}}$,
则tan(A+$\frac{π}{4}$)=$\frac{tanA+1}{1-tanA}$=$\frac{2}{1-tanA}$-1≤$\frac{2}{1-\frac{1}{2\sqrt{2}}}$-1=$\frac{9+4\sqrt{2}}{7}$.
∴tan(A+$\frac{π}{4}$)的最大值为$\frac{9+4\sqrt{2}}{7}$.
故答案为:$\frac{9+4\sqrt{2}}{7}$.
点评 本题考查了正弦定理、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
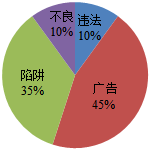 2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.
2014年春晚唱响的一曲“群发的我不回”让短信再次成为关注焦点,手机短信中不乏大量垃圾短信,垃圾短信一般分为不良短信、广告短信、违法短信、陷阱短信等四类,其分布如图.| 条数 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25) | [25,30) |
| 人数 | 1 | 2 | 5 | 9 | 5 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com