
| A. | (-∞,4] | B. | (-∞,6] | C. | [-4,+∞) | D. | [6,+∞) |
分析 根据一次函数,以及导数研究函数f(x)的单调性,求出函数f(x)与g(x)的值域,根据恒成立关系转化为两个函数的值域问题,进行求解即可.
解答 解:当$\frac{1}{2}$<x≤1时,f(x)=$\frac{2{x}^{3}}{x+1}$,则f′(x)=$\frac{2{x}^{2}(2x+3)}{(x+1)^{2}}$>0,此时函数为增函数,
则f($\frac{1}{2}$)<f(x)≤f(1),
即$\frac{1}{6}$<f(x)≤1,
当0≤x≤$\frac{1}{2}$时,f(x)=$\frac{x}{3}$为增函数,
则0≤f(x)≤$\frac{1}{6}$,
综上所述,当x∈[0,1]时,0≤f(x)≤1,
当x2$∈[0,\frac{1}{2}]$,g(0)≤g(x)≤g($\frac{1}{2}$),
即3-$\frac{a}{2}$≤g(x)≤3,
若对任意x1∈[0,1],总存在x2$∈[0,\frac{1}{2}]$,使得f(x1)=g(x2)成立,
则[0,1]⊆[3-$\frac{a}{2}$,3],则3-$\frac{a}{2}$≤0,即$\frac{a}{2}$≥3,
则a≥6,
故实数a的取值范围是[6,+∞),
故选:D.
点评 本题主要考查函数恒成立问题,根据导数研究函数的单调性,求出函数的值域,根据条件建立值域之间的关系是解决本题的关键.综合考查学生是运算和推理能力.


科目:高中数学 来源: 题型:解答题
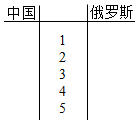 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
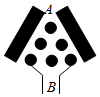 将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.
将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 3 | 2 | 5 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄x | 21 | 24 | 34 | 41 |
| 脂肪y | 9.5 | 17.5 | 24.9 | 28.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
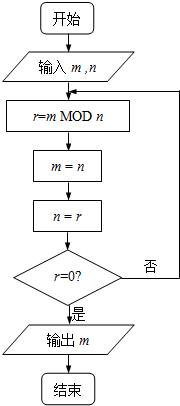 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )| A. | 0 | B. | 5 | C. | 45 | D. | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com