
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 3 | 2 | 5 | 4 |
分析 (Ⅰ)记“3人答对题目个数之和为6”为事件A,利用排列组合知识能求出3人答对题目个数之和为6的概率.
(Ⅱ)由题意知X的所有取值为0,1,2,3,4,5,6,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)记“3人答对题目个数之和为6”为事件A,
则P(A)=$\frac{{C}_{5}^{3}+{C}_{2}^{1}{C}_{5}^{1}{C}_{4}^{1}}{{C}_{14}^{3}}$=$\frac{17}{91}$,
∴3人答对题目个数之和为6的概率p=$\frac{17}{91}$.
(Ⅱ)由题意知X的所有取值为0,1,2,3,4,5,6,
则P(X=0)=$\frac{{C}_{3}^{2}}{{C}_{14}^{2}}$=$\frac{3}{91}$,
P(X=1)=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{{C}_{14}^{2}}$=$\frac{6}{91}$,
P(X=2)=$\frac{{C}_{2}^{2}+{C}_{3}^{1}{C}_{5}^{1}}{{C}_{14}^{2}}$=$\frac{16}{91}$,
P(X=3)=$\frac{{C}_{3}^{1}{C}_{4}^{1}+{C}_{2}^{1}{C}_{5}^{1}}{{C}_{14}^{2}}$=$\frac{22}{91}$,
P(X=4)=$\frac{{C}_{5}^{2}+{C}_{2}^{1}{C}_{4}^{1}}{{C}_{14}^{2}}$=$\frac{18}{91}$,
P(X=5)=$\frac{{C}_{5}^{1}{C}_{4}^{1}}{{C}_{14}^{2}}$=$\frac{20}{91}$,
P(X=6)=$\frac{{C}_{4}^{2}}{{C}_{14}^{2}}$=$\frac{6}{91}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | $\frac{3}{91}$ | $\frac{6}{91}$ | $\frac{16}{91}$ | $\frac{22}{91}$ | $\frac{18}{91}$ | $\frac{20}{91}$ | $\frac{6}{91}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $1-\frac{1}{e}$ | B. | $\frac{e+1}{e^2}$ | C. | $\frac{1}{e}$ | D. | $\frac{e-1}{e^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x≤-1或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (-∞,6] | C. | [-4,+∞) | D. | [6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
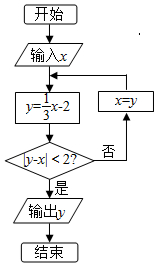 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )| A. | -$\frac{23}{9}$ | B. | 1 | C. | $\frac{8}{9}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M | B. | N | C. | {x|-1≤x≤2} | D. | {x|-3≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com