
分析 (1)根据对数函数的性质,求出函数g(x)的最小值大0,解不等式即可;
(2)根据复合函数的单调性得到g(x)的最小值是2,求出a的值即可;
(3)结合函数的单调性得到关于a的不等式组,解出即可.
解答 解:记g(x)=x2-2ax+3=(x-a)2+3-a2,
(1)由题意知g(x)>0对x∈R恒成立,
∴$g{(x)_{min}}=3-{a^2}>0$
解得$-\sqrt{3}<a<\sqrt{3}$
∴实数a的取值范围是$(-\sqrt{3},\sqrt{3})$.-----------(4分)
(2)由函数$y={log_{\frac{1}{2}}}u$是减函数及函数$f(x)={log_{\frac{1}{2}}}({x^2}-2ax+3)$的值域为(-∞,-1]
可知 x2-2ax+3≥2.
由(1)知g(x)的值域为[3-a2,+∞),
∴$g{(x)_{min}}=3-{a^2}=2$.
∴a=±1.-----------(8分)
(3)由题意得$\left\{\begin{array}{l}a≥1\\{1^2}-2a×1+3≥0\end{array}\right.$,解得1≤a≤2,
∴实数a的取值范围是[1,2].-----------(12分)
点评 本题考查了对数函数、二次函数的性质,考查复合函数的单调性问题,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
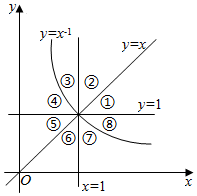 如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )
如图,函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分:①②③④⑤⑥⑦⑧.若幂函数f(x)的图象经过的部分是④⑧,则f(x)可能是( )| A. | y=x2 | B. | $y=\frac{1}{{\sqrt{x}}}$ | C. | $y={x^{\frac{1}{2}}}$ | D. | y=x-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com