
分析 充分利用面面垂直和面面平行的性质定理对选项分别分析选择.
解答 解:对于①,α∩β=l,m与α,β所成角相等,当m∥α,β时,m∥l,得不到l⊥m;
对于②,α⊥β,l⊥α,得到l∥β或者l?β,又m∥β,所以l与m不一定垂直;
对于③,l,m与平面α所成角之和为90°,当l,m与平面α都成45°时,可能平行,故③错误;
对于④,α∥β,l⊥α,得到l⊥β,又m∥β,所以l⊥m;
对于⑤,PA⊥α于A,P∈l,l∩α=B(B不同于P),m?α,AB⊥m,根据三垂线定理可得正确.
故答案为:④⑤.
点评 本题考查了直线垂直的判断,用到了线面垂直、线面平行的性质定理和判定定理,熟练运用相关的定理是关键,属于中档题目.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
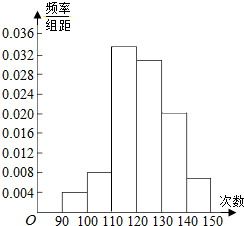 为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.
为了了解高一学生的体能情况,某校抽取部分学生进行一部分跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12,若次数在110以上(含110次)为达标,试估计该学校全体高一学生单调达标率是0.88.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (4,+∞) | C. | (0,$\frac{1}{4}$] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}]$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | C. | (3,0) | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com