
分析 对a的大小关系分类讨论,利用一元二次不等式的解法即可得出.
解答 解:原不等式化为(x-2)(ax-2)>0,
①当a=0时,原不等式化为x-2<0,解得x<2;
②当0<a<1时,原不等式化为$(x-2)(x-\frac{2}{a})>0$,且$2<\frac{2}{a}$,
解得$x>\frac{2}{a}$或x<2;
③当a=1时,原不等式化为(x-2)2>0,解得x∈R且x≠2;
④当1<a<2时,原不等式化为$(x-2)(x-\frac{2}{a})>0$,且$2>\frac{2}{a}$,
解得$x<\frac{2}{a}$或x>2;
综上所述,当a=0时,原不等式的解集为{x|x<2};
当0<a≤1时,原不等式的解集为$\left\{{x|}\right.x>\frac{2}{a}$或x<2};
当1<a<2时,原不等式的解集为{x|x>2或$x<\frac{2}{a}\left.{\;}\right\}$.
点评 本题考查了一元二次不等式的解法,考查了分类讨论的思想方法,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不认真听讲 | 能认真听讲 | 总计 | |
| 15周岁以下 | |||
| 15周岁以上 | |||
| 总计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意a,P1是P2的子集,对任意b,Q1不是Q2的子集 | |
| B. | 对任意a,P1是P2的子集,存在b,使得Q1是Q2的子集 | |
| C. | 存在a,P1不是P2的子集,对任意b,Q1不是Q2的子集 | |
| D. | 存在a,P1不是P2的子集,存在b,使得Q1是Q2的子集 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
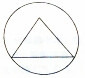 棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)在(0,$\frac{π}{4}$)上单调递增,且为奇函数 | |
| B. | g(x)的最大值为1,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | g(x)在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,且为偶函数 | |
| D. | g(x)的周期为π,其图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com