
分析 (1)不等式f(x)<2,即|2x+1|<2,由此求得不等式的解集.
(2)由题意可得存在实数x,使得|x+$\frac{1}{2}$|-|x|≤1+$\frac{a}{2}$ 成立,再根据绝对值的意义可得|x+$\frac{1}{2}$|-|x|的最小值为-$\frac{1}{2}$,故有-$\frac{1}{2}$≤1+$\frac{a}{2}$,由此求得a的范围.
解答 解:(1)不等式f(x)<2,即|2x+1|<2,即-2<2x+1<2,
求得-$\frac{3}{2}$<x<$\frac{1}{2}$,故不等式的解集为(-$\frac{3}{2}$,$\frac{1}{2}$).
(2)由题意可得f(x)≤g(x),即|x+$\frac{1}{2}$|-|x|≤1+$\frac{a}{2}$,
而|x+$\frac{1}{2}$|-|x|表示数轴上的x对应点到-$\frac{1}{2}$对应点的距离减去它到原点的距离,它的最小值为-$\frac{1}{2}$,
再根据存在实数x,使得f(x)≤g(x),故有-$\frac{1}{2}$≤1+$\frac{a}{2}$,求得 a≥-3.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的能成立问题,体现了转化的数学思想,属于基础题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=$\sqrt{{x}^{2}+2}$+$\frac{1}{\sqrt{{x}^{2}+2}}$ | D. | y=tanx+$\frac{1}{tanx}$(0<x<$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
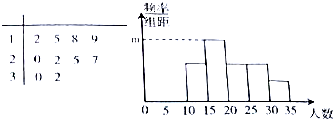 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com