分析:(1)欲证AB1∥平面BC1D,只需证明AB1平行平面BC1D中的一条直线,利用三角形的中位线平行与第三边,构造一个三角形AB1C,使AB1成为这个三角形中的边,而中位线OD恰好在平面BC1D上,就可得到结论.
(2)先根据AA1=AB=2,四棱锥B-AA1C1D的体积为3,求出BC长,利用三垂线定理,取BC中点M,连接DM,DM⊥平面BCC1,作MN⊥NC1与N,连接DN,则DN⊥BC1,则∠DNM为二面角C-BC1-D的平面角.再把角∠DNM放到三角形DMN中求出正切值即可.
解答:解:(1)证明:连接B
1C,设B
1C与BC
1相交于点O,连接OD,
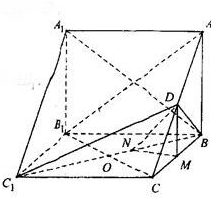
∵四边形BCC
1B是平行四边形,∴点O为B
1C的中点,
∵D为AC的中点,∴OD为△AB
1C的中位线,∴OD∥AB
1,
∵OD?平面BC
1D,AB
1?平面BC
1D,∴AB
1∥平面BC
1D
(2)依题意知,AB=BB
1=2,∵AA
1⊥底面ABC,AA
1?底面AA
1C
1C,
∴平面ABC⊥平面AA
1C
1C,且平面ABC∩平面AA
1C
1C=AC
作BE⊥AC,垂足为E,则BE⊥平面AA
1C
1C.
设BC=a,在Rt△ABC中,BE=
=
∴四棱锥B-AA
1C
1D的体积V=
×
(A
1C
1+AD)•AA
1•BE=a=3,即BC=3
取BC中点M,连接DM,DM⊥平面BCC
1,作MN⊥NC
1与N,连接DN,则DN⊥BC
1,
∠DNM为二面角C-BC
1-D的平面角.
在△DMN中,DM=1,MN=
,tan∠DNM=
,
∴二面角C-BC
1-D的正切值为
点评:本题考察了线面平行判定定理的应用和二面角的作法和求法,解决二面角问题是要按照一作二证三计算的步骤,准确规范解题

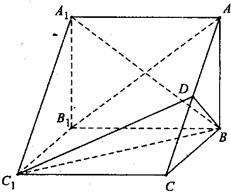 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.


 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.