
如图,在四棱锥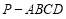 中,
中,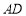 //
// ,
,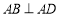 ,
,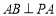 ,
,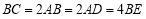 ,平面
,平面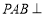 平面
平面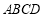 .
.
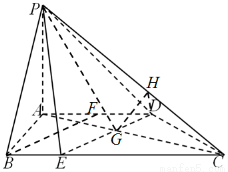
(1)求证:平面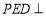 平面
平面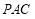 ;
;
(2)若直线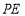 与平面
与平面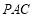 所成的角的正弦值为
所成的角的正弦值为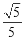 ,求二面角
,求二面角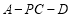 的平面角的余弦值.
的平面角的余弦值.
(1)见解析;(2)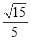
【解析】试题分析:(1)证明面面垂直的基本思路,是在其中一个面内,找一条直线垂直于另一个平面内两条相交直线,本题只需证明ED⊥PA,ED⊥AC即可;(2)重点是找二面角的平面角,即在两个面内分别找垂直于交线的直线,然后构造三角形求解。当然,利用空间向量也是解决本题的好办法。
试题解析:法一(1)取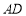 中点
中点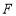 ,连接
,连接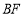 ,则
,则 ,
,
∴四边形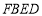 是平行四边形,∴
是平行四边形,∴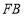 //
//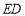
∵直角△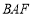 和直角△
和直角△ 中,
中,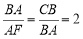
∴直角△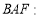 直角△
直角△ ,易知
,易知
∴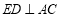
∵平面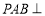 平面
平面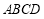 ,平面
,平面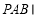 平面
平面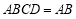

∴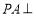 平面
平面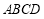
∴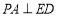 ,
,
∵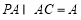
∴ 平面
平面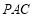 .
.
∴平面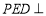 平面
平面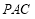 .
.
(2)设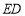 交
交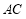 于
于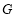 ,连接
,连接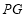 ,则
,则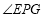 是直线
是直线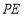 与平面
与平面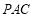 所成的角.设
所成的角.设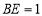
由△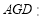 △
△ ,知
,知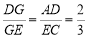 ,
,
∵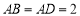
∴ ,
,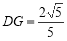
∵∴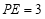 ,
,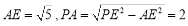
作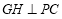 于
于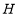 ,由
,由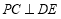 ,知
,知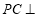 平面
平面 ,
,
∴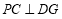 ,
,
∴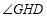 是二面角
是二面角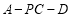 的平面角.
的平面角.
∵△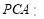 △
△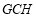 ,
,
∴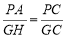 ,而
,而
∴
∴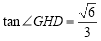 ,
,
∴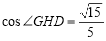 ,
,
即二面角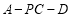 的平面角的余弦值为
的平面角的余弦值为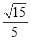 .
.
法二:(1)∵平面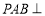 平面
平面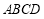 ,
,
平面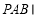 平面
平面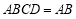 ,
,
∴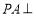 平面
平面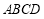
又∵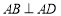 ,故可如图建立空间直角坐标系
,故可如图建立空间直角坐标系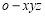
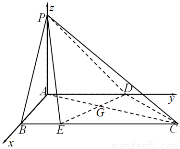
由已知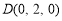 ,
,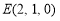 ,
,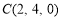 ,
,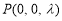 (
(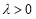 )
)
∴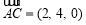 ,
,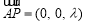 ,
,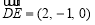
∴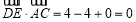 ,
,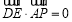 ,
,
∴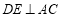 ,
,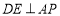 ,
,
∴ 平面
平面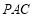
∴平面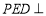 平面
平面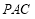
(2)由(1),平面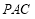 的一个法向量是
的一个法向量是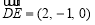 ,
,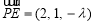
设直线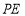 与平面
与平面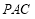 所成的角为
所成的角为 ,
,
∴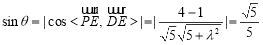 ,
,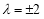
∵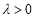
∴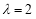 ,即
,即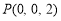
设平面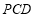 的一个法向量为
的一个法向量为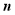
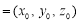 ,
,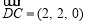 ,
,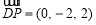
由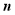
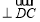 ,
,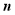
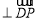
∴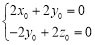 ,令
,令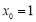 ,则
,则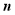
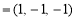
∴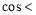
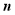 ,
,
显然二面角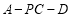 的平面角是锐角,
的平面角是锐角,
∴二面角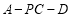 的平面角的余弦值为
的平面角的余弦值为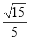
考点:空间几何体,线面位置关系


科目:高中数学 来源: 题型:
|
|
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
设f(x)=4sinxsin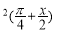 +cos2x,|f(x)-m|<3对?x∈(0,π)恒成立,则实数m的范围是( )
+cos2x,|f(x)-m|<3对?x∈(0,π)恒成立,则实数m的范围是( )
A.[0,4] B.(0,4] C.[0,4) D.(0,4)
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
对任意等比数列{an},下列说法一定正确的是( )
A.a1,a3,a9成等比数列
B.a2,a3,a6成等比数列
C.a2,a4,a8成等比数列
D.a3,a6,a9成等比数列
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
已知函数f(x)=xn+1(n∈N*)的图象与直线x=1交于点P,若图象在点P处的切线与x轴交点的横坐标为xn,则log2014x1+log2014x2+…+log2014x2013的值为( )
A.﹣1 B.1﹣log20142013 C.﹣log20142013 D.1
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
若p:x2﹣4x+3>0;q:x2<1,则p是q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
在正方体ABCD-A'B'C'D'中,点P在线段AD'上运动,则异面直线CP与BA'所成的角θ的取值范围是 ( )

A. B.
B.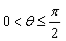 C.
C. 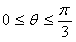 D.
D.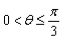
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com