练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在如图所示的长方体ABCD-A1B1C1D1中，已知A1（a，0，c），C（0，b，0），则点B1的坐标为（a，b，c）．

    分析 由如图所示所建立的空间直角坐标系，以及A1，C的坐标，可以得知该长方形的长，宽，高，进而可以得知B1的点坐标．

    解答 解：∵在如图所示的长方体ABCD-A1B1C1D1中，已知A1（a，0，c），C（0，b，0），
    ∴可以得知AD=a，DC=b，DD1=c，
    又∵长方体ABCD-A1B1C1D1，
    ∴可以得知B1的坐标为（a，b，c）
    故答案为：（a，b，c）．

    点评 本题考查空间直角坐标系的定义以及由点坐标得出长方形的长度参量，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．连续掷一枚骰子两次，则两次骰子正面向上的点数之和为奇数的概率为（　　）
    A．$\frac{5}{12}$B．$\frac{4}{9}$C．$\frac{1}{2}$D．$\frac{7}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．某人对一地区人均工资x（千元）与该地区人均消费y（千元）进行统计调查，y与x有相关关系，得到回归直线方程$\hat y$=0.66x+1.56．若该地区的人均消费水平为7.5千元，则该地区的人均工资收入为9（千元）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

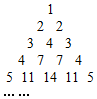    11．用部分自然数构造如图的数表：用aij（i≥j）表示第i行第j个数（i，j∈N+），使得ai1=aii=i．每行中的其他各数分别等于其“肩膀”上的两个数之和，a（i+1）j=ai（j-1）+aij（i≥2，j≥2）．设第n（n∈N+）行的第二个数为bn（n≥2）．
    （1）写出第7行的第三个数； 
    （2）写出bn+1与bn的关系并求bn（n≥2）；
    （3）设cn=2（bn-1）+n，证明：$\frac{1}{c_2}$+$\frac{1}{c_4}$+$\frac{1}{c_6}$+…+$\frac{1}{{{c_{2n}}}}$＜$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设有一正态总体，它的概率密度曲线是函数y=f（x）的图象，且f（x）=$\frac{1}{{\sqrt{8π}}}{e^{-\frac{{{{（x-10）}^2}}}{8}}}$，则这个正态总体的期望与标准差分别是（　　）
    A．10与4B．10与2C．4与10D．2与10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知随机变量ξ的分布列为
    ξ-2-10123
    P$\frac{1}{12}$$\frac{3}{12}$$\frac{4}{12}$$\frac{1}{12}$$\frac{2}{12}$$\frac{1}{12}$
    若P（ξ2＞x）=$\frac{1}{12}$，则实数x的取值范围是[4，9）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．一个盒子里装有三张卡片，分别标记有数字1，2，3，这三张卡片除标记的数字外完全相同，从中随机有放回地抽取3次，每次抽取1张，求下列事件的概率．
    （1）求“抽取的卡片上的数字满足其中两张之和等于第三张”的概率；
    （2）求“抽取的卡片上的数字不完全相同”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知等比数列{an}的公比q=2，且a2，a3+1，a4成等差数列．
    （1）求a1及an；
    （2）设bn=an+n，求数列{bn}的前5项和S5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

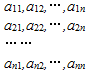    12．设A1，A2，…，An（n≥4）为集合S={1，2，…，n}的n个不同子集，为了表示这些子集，作n行n列的数阵，规定第i行第j列的数为：${a_{ij}}=\left\{\begin{array}{l}0，\;i∉{A_j}\\ 1，\;i∈{A_j}\end{array}\right.$．则下列说法中，错误的是（　　）
    A．数阵中第一列的数全是0当且仅当A1=∅
    B．数阵中第n列的数全是1当且仅当An=S
    C．数阵中第j行的数字和表明集合Aj含有几个元素
    D．数阵中所有的n2个数字之和不超过n2-n+1

    查看答案和解析>>

    同步练习册答案