
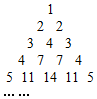 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).分析 (1)直接计算即得结论;
(2)通过对bn+1=bn+n变形可知bn+1-bn=n,进而累加计算即得结论;
(3)通过(2)可知cn=n2,放缩可知$\frac{1}{{c}_{2k}}$<$\frac{1}{2}$($\frac{1}{2k-1}$-$\frac{1}{2k+1}$),进而累加计算即得结论.
解答 (1)解:第7行的第三个数为41;
(2)解:由已知得bn+1=bn+n,
∴当n≥2时,b3-b2=2,b4-b3=3,…,bn+1-bn=n,
累加,得:bn+1-b2=2+3+4+…+n,
∴bn+1=1+(1+2+3+4+…+n)=1+$\frac{n(n+1)}{2}$,
∴${b_n}=1+\frac{n(n-1)}{2}({n≥2})$;
(3)证明:由(2)${c_n}=2({{b_n}-1})+n={n^2}$,
∵$\frac{1}{{{c_{2k}}}}=\frac{1}{{4{k^2}}}<\frac{1}{{4{k^2}-1}}=\frac{1}{2}({\frac{1}{2k-1}-\frac{1}{2k+1}})$,
∴$\frac{1}{c_2}+\frac{1}{c_4}+\frac{1}{c_6}+…+\frac{1}{{{c_{2n}}}}<\frac{1}{2}({1-\frac{1}{3}})+\frac{1}{2}({\frac{1}{3}-\frac{1}{5}})+…\frac{1}{2}({\frac{1}{2n-1}-\frac{1}{2n+1}})$=$\frac{1}{2}({1-\frac{1}{2n+1}})<\frac{1}{2}$.
点评 本题是一道关于数列与不等式的综合题,考查累加法、裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
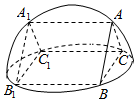 如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )
如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com