
| X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
分析 (1)由某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据表,能求出$\overline x$,$\overline y$.
(2)由某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据表,能作出散点图.
(3)由散点图知,y与x有线性相关关系.设回归直线方程:$\widehat{y}$=bx+a,由此能求出线性回归方程.
解答 解:(1)$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,
$\overline{y}$=$\frac{1}{7}$(66+69+73+81+89+90+91)=79.86.
(2)由某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据表,
作出散点图如下:
(3)由散点图知,y与x有线性相关关系.
设回归直线方程:$\widehat{y}$=bx+a,
∵x12+x22+…+x72=280,x1y1+x2y2+…+x7y7=3487.
${{y}_{1}}^{2}$+${{y}_{2}}^{2}$+…+${{y}_{7}}^{2}$=45 309,$\overline{x}$=6,$\overline{y}$=79.86,
∴b=$\frac{3487-7×6×\frac{559}{7}}{280-7×36}$=4.75.
a=79.86-6×4.75=51.36,
∴回归直线方程$\widehat{y}$=4.75x+51.36.
点评 本题考查平均数的求法,考查散点图的作法,考查线性回归直线方程的求法,是中档题,解题时要认真审题,注意线性回归方程的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0>8 | B. | 0<x0≤1或x0>8 | C. | 0<x0<8 | D. | -1<x0<0或0<x0<8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
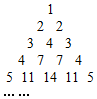 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com