
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=$-\frac{{\sqrt{2}}}{2}sin(2x-\frac{π}{4})+\frac{1}{2}$,利用周期公式即可得解f(x)的最小正周期;
(2)令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,k∈Z,即可求得函数f(x)的单调递增区间.
(3)由$0≤x≤\frac{π}{2}$,得$-\frac{π}{4}≤2x-\frac{π}{4}≤\frac{3π}{4}$,进而可得$-\frac{{\sqrt{2}}}{2}≤sin(2x-\frac{π}{4})≤1$,利用正弦函数的图象和性质即可得解.
解答 (本题满分为12分)
解:(1)f(x)=cos2x-sinxcosx
=$\frac{1+cos2x}{2}-\frac{1}{2}sin2x$…3分
=$-\frac{1}{2}(sin2x-cos2x)+\frac{1}{2}$
=$-\frac{{\sqrt{2}}}{2}sin(2x-\frac{π}{4})+\frac{1}{2}$,…5分
所以f(x)的最小正周期$T=\frac{2π}{2}=π$.…6分
(2)令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得:kπ+$\frac{3π}{8}$≤x≤kπ+$\frac{7π}{8}$,k∈Z,
可得函数f(x)的单调递增区间为:[kπ+$\frac{3π}{8}$,kπ+$\frac{7π}{8}$],k∈Z.…7分
(3)由$0≤x≤\frac{π}{2}$,得$-\frac{π}{4}≤2x-\frac{π}{4}≤\frac{3π}{4}$,
所以$-\frac{{\sqrt{2}}}{2}≤sin(2x-\frac{π}{4})≤1$,…8分
所以当$2x-\frac{π}{4}=-\frac{π}{4}$,即x=0时,$f{(x)_{max}}=-\frac{{\sqrt{2}}}{2}×(-\frac{{\sqrt{2}}}{2})+\frac{1}{2}=1$; …10分
当$2x-\frac{π}{4}=\frac{π}{2}$,即$x=\frac{3π}{8}$时,$f{(x)_{min}}=-\frac{{\sqrt{2}}}{2}×1+\frac{1}{2}=\frac{{1-\sqrt{2}}}{2}$.…12分.
点评 本题主要考查了三角函数恒等变换的应用,周期公式,正弦函数的图象和性质,考查了转化思想,属于基础题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
| 非重度污染 | 严重污染 | 合计 | |
| 供暖季 | 22 | 8 | 30 |
| 非供暖季 | 63 | 7 | 70 |
| 合计 | 85 | 15 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
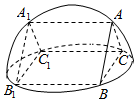 如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )
如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知一个锥体挖去一个柱体后的三视图如图所示,网格上小正方形的边长为1,则该几何体的体积等于( )
已知一个锥体挖去一个柱体后的三视图如图所示,网格上小正方形的边长为1,则该几何体的体积等于( )| A. | 11π | B. | 5π | C. | $\frac{11}{3}$π | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com