
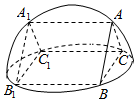
 如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )
如图,直三棱柱ABC-A1B1C1的六个顶点都在半径为2的半球面上,AB=AC,侧面BCC1B1是半球底面圆的内接正方形,则侧面ABB1A1的面积为( )| A. | $4\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 判断球心的位置,利用侧面BCC1B1是半球底面圆的内接正方形,R=2,求出OC=$\sqrt{2}$,OA=2,利用勾股定理求出AB,然后求解四边形的面积.
解答 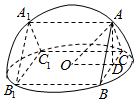 解:如图所示,球心在平面BCC1B1的中心O上
解:如图所示,球心在平面BCC1B1的中心O上
取BC的中点D,连接AD,OD,则AD⊥BC
∵侧面BCC1B1是半球底面圆的内接正方形,R=2,
∴OC=$\sqrt{2}$,OA=2
∴AC=$\sqrt{2}$,
∴AB=$\sqrt{2+2}$=2,
∴侧面ABB1A1的面积为2$•2\sqrt{2}$=4$\sqrt{2}$
故选:A.
点评 本题考查与球有关的几何体的问题,考查勾股定理,空间点、线、面的位置关系的应用.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
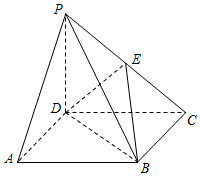 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
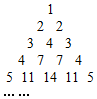 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com