
分析 由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,所以可在其每个面补上一个以a,2,2为三边的三角形作为底面,且以分别为x,y,z,长、两两垂直的侧棱的三棱锥,从而可得到一个长、宽、高分别为x,y,z的长方体,由此能求出球的半径,进而利用四面体ABCD的外接球的表面积为7π,求出a.
解答 解:由题意可采用割补法,考虑到四面体ABCD的四个面为全等的三角形,
所以可在其每个面补上一个以a,2,2为三边的三角形作为底面,
且以分别为x,y,z,长、两两垂直的侧棱的三棱锥,
从而可得到一个长、宽、高分别为x,y,z的长方体,
并且x2+y2=a2,x2+z2=4,y2+z2=4,
设球半径为R,则有(2R)2=x2+y2+z2=$\frac{1}{2}$a2+4,
∵四面体ABCD的外接球的表面积为7π,
∴球的表面积为S=4πR2=7π.
∴4R2=7,
∴$\frac{1}{2}$a2+4=7,∴a=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查几何体的外接球的表面积的求法,割补法的应用,判断外接球的直径是长方体的对角线的长是解题的关键之一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
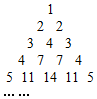 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aii=i.每行中的其他各数分别等于其“肩膀”上的两个数之和,a(i+1)j=ai(j-1)+aij(i≥2,j≥2).设第n(n∈N+)行的第二个数为bn(n≥2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com