
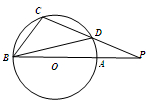
 如图,AB是半径为3的⊙O的直径,CD是弦,BA,CD的延长线交于点P,PA=4,PD=5,则∠CBD=
如图,AB是半径为3的⊙O的直径,CD是弦,BA,CD的延长线交于点P,PA=4,PD=5,则∠CBD=

科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).
某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).查看答案和解析>>
科目:高中数学 来源: 题型:
| 患支气管炎 | 为患支气管炎 | 总计 | |
| 吸烟 | 43 | 162 | 205 |
| 不吸烟 | 13 | 121 | 134 |
| 总计 | 56 | 283 | 339 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com