
已知二次函数 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且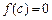 ,当
,当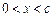 时,恒有
时,恒有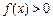 .
.
(1)当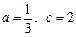 时,求不等式
时,求不等式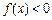 的解集;
的解集;
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,且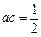 ,求a的值;
,求a的值;
(3)若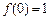 ,且
,且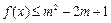 对所有
对所有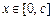 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)一块边长为10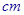 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积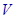 与
与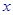 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要 维护费50元.
维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多 少?
少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14 分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率
分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率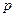 与每日生产产品件数
与每日生产产品件数 (
(
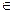
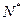 )间的关系为
)间的关系为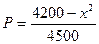 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%)
(Ⅰ)将日利润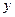 (元)表示成日产量
(元)表示成日产量 (件)的函数;
(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知某商品的价格上涨x%,销售的数量就减少mx%,其中m为正的常数。
(1)当m=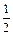 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)已知二次函数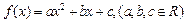 满足:对任意实数x,都有
满足:对任意实数x,都有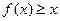 ,且当
,且当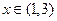 时,有
时,有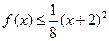 成立.
成立.
(1)求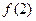 ;
;
(2)若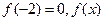 的表达式;
的表达式;
(3)设 ,若
,若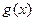 图上的点都位于直线
图上的点都位于直线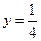 的上方,求实
的上方,求实
数m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com