
分析 (1)f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x,x∈(-∞,0]}\\{-a{x}^{2}+x,x∈(0,+∞)}\end{array}\right.$,作其图象,从而利用数形结合求解得a∈(0,$\frac{1}{2}$);从而可得x2+x3=$\frac{1}{a}$,x1=$\frac{-1-\sqrt{1+4{a}^{2}}}{2a}$,从而求得;
(2)显然,f(x)为R上的奇函数,从而可得M=2,再分类讨论求最大值即可.
解答 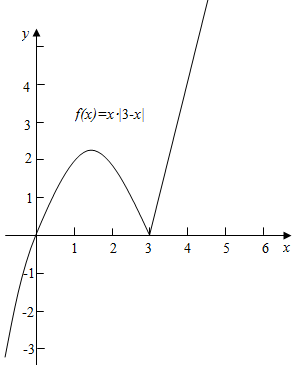 解:(1)f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x,x∈(-∞,0]}\\{-a{x}^{2}+x,x∈(0,+∞)}\end{array}\right.$,
解:(1)f(x)=$\left\{\begin{array}{l}{a{x}^{2}+x,x∈(-∞,0]}\\{-a{x}^{2}+x,x∈(0,+∞)}\end{array}\right.$,
当a>0时,其图象如右图所示,
∵直线y=a与y=f(x)的图象有三个不同的交点,
∴f($\frac{1}{2a}$)>a>0,即$\frac{1}{4a}$>a>0,
解得,a∈(0,$\frac{1}{2}$);
其次,由韦达定理及求根公式可得,
x2+x3=$\frac{1}{a}$,x1=$\frac{-1-\sqrt{1+4{a}^{2}}}{2a}$,
从而可得,$\frac{{x}_{1}}{{x}_{2}+{x}_{3}}$=-$\frac{\sqrt{1+4{a}^{2}}+1}{2}$,
注意到a∈(0,$\frac{1}{2}$),
∴$\frac{{x}_{1}}{{x}_{2}+{x}_{3}}$∈(-$\frac{\sqrt{2}+1}{2}$,-1).
(2)显然,f(x)为R上的奇函数,
∴M-m=2M=4,
当a=0时,经检验不符合题意,舍去;
当a<0时,函数f(x)在[-1,1]上单调递增,
故M=f(1)=1-a=2,
故a=-1;
当a>0时,f(x)在(-∞,-$\frac{1}{2a}$)和($\frac{1}{2a}$,+∞)上单调递减,
在(-$\frac{1}{2a}$,$\frac{1}{2a}$)上单调递增;
①当$\frac{1}{2a}$≥1,即0<a≤$\frac{1}{2}$时,f(x)[-1,1]上单调递增,
可解得a=-1(舍去),
②当$\frac{1}{2a}$<1,即$\frac{1}{2}$<a<1时,f(x)在[-1,1]上的最大值为f($\frac{1}{2a}$)=$\frac{1}{4a}$=2,
解得,a=$\frac{1}{8}$(舍去);
综上所述,a=-1.
点评 本题考查了分类讨论的思想与数形结合的思想应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
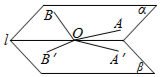 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )| A. | ∠A′OB′为钝角 | B. | ∠A′OB′>∠AOB | ||
| C. | ∠AOB+∠AOA′<π | D. | ∠B′OB+∠BOA+∠AOA′>π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
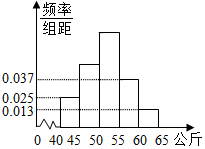 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{π}^{2}}{4}$-1 | B. | $\frac{3{π}^{2}}{16}$-1 | C. | $\frac{3{π}^{2}}{4}$-1 | D. | $\frac{{π}^{2}}{8}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com