
���� ��1����ԲC�IJ���������ȥt�õ�ԲC����ͨ���̣���ֱ��l�ļ����귽�̣��������Ǻ��������Һ�����ʽ������x=��cos�ȣ�y=��sin��ת��Ϊֱ�����귽�̼��ɣ�
��2����A��B�ļ����껯Ϊֱ�����꣬�����|AB|�ij�������P��ԲC�ϣ����P���꣬���õ㵽ֱ�ߵľ��빫ʽ��ʾ��P��ֱ��l�ľ��룬�������Һ�����ֵ��ȷ������Сֵ������ȷ����������PAB�������Сֵ��
��� �⣺��1����$\left\{\begin{array}{l}{x=-5+\sqrt{2}cost}\\{y=3+\sqrt{2}sint}\end{array}\right.$������ã�$\left\{\begin{array}{l}{x+5=\sqrt{2}cost}\\{y-3=\sqrt{2}sint}\end{array}\right.$��
��ȥ����t���ã�x+5��2+��y-3��2=2��
��ԲC����ͨ����Ϊ��x+5��2+��y-3��2=2��
�ɦ�cos����+$\frac{��}{4}$��=-$\sqrt{2}$�������$\frac{\sqrt{2}}{2}$��cos��-$\frac{\sqrt{2}}{2}$��sin��=-$\sqrt{2}$��
����cos��-��sin��=-2����x-y+2=0��
��ֱ��l��ֱ�����귽��Ϊx-y+2=0��
����A��2��$\frac{��}{2}$����B��2���У���Ϊֱ������ΪA��0��2����B��-2��0����
��|AB|=$\sqrt{��0+2��^{2}+��2-0��^{2}}$=2$\sqrt{2}$��
��P���������-5+$\sqrt{2}$cost��3+$\sqrt{2}$sint����
��P�㵽ֱ��l�ľ���Ϊd=$\frac{|-5+\sqrt{2}cost-3-\sqrt{2}sint+2|}{\sqrt{2}}$=$\frac{{|{-6+2cos��{t+\frac{��}{4}}��}|}}{{\sqrt{2}}}$��
��dmin=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$��
���PAB�������Сֵ��S=$\frac{1}{2}$��2$\sqrt{2}$��2$\sqrt{2}$=4��
���� ���⿼����Բ�IJ������̣��Լ������ߵļ����귽�̣��������ղ�����������ͨ���̼��ת���ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 16cm3 | B�� | 20cm3 | C�� | 24cm3 | D�� | 30cm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=1����=$\frac{��}{3}$ | B�� | a=1����=$\frac{��}{6}$ | C�� | a=$\sqrt{3}$����=$\frac{��}{3}$ | D�� | a=$\sqrt{3}$����=$\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
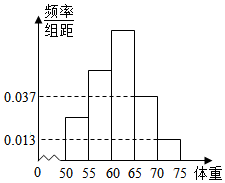 Ϊ�˽����ijУ������ҵ������������Աѧ������������������õ���������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12��
Ϊ�˽����ijУ������ҵ������������Աѧ������������������õ���������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com