
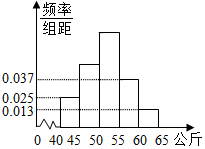
 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.分析 (Ⅰ)设该校抽查的学生总人数为n,第2组、第3组的频率分别为p2,p3,先求出p3,由此能求出n,由p2+0.375+(0.025+0.013+0.037)×5=1,求出p2,由此能求出该校抽查的学生总人数和从左到右第2组的频率.
(Ⅱ)由(Ⅰ)知:体重不低于55公斤的学生的概率为$\frac{1}{4}$,X服从二项分布$X~B(5,\frac{1}{4})$,由此能求出随机变量X的分布列和数学期望.
解答 (本小题满分12分)
(Ⅰ)设该校抽查的学生总人数为n,第2组、第3组的频率分别为p2,p3,
则p3=0.025×3×5=0.375,所以$n=\frac{90}{p_3}=240$,(3分)
由p2+0.375+(0.025+0.013+0.037)×5=1,解得p2=0.25,
所以该校抽查的学生总人数为240人,从左到右第2组的频率为0.25.(6分)
(Ⅱ)由(Ⅰ)知:体重不低于55公斤的学生的概率为$p=(0.013+0.037)×5=\frac{1}{4}$,(8分)
X服从二项分布$X~B(5,\frac{1}{4})$,$p(X=k)=C_5^k{(\frac{1}{4})^k}{(\frac{3}{4})^{5-k}}$,k=0,1,2,3,4,5,(9分)
P(X=0)=${C}_{5}^{0}(\frac{3}{4})^{5}=\frac{243}{1024}$,
P(X=1)=${C}_{5}^{1}(\frac{1}{4})(\frac{3}{4})^{4}=\frac{405}{1024}$,
P(X=2)=${C}_{5}^{2}(\frac{1}{4})^{2}(\frac{3}{4})^{3}$=$\frac{270}{1024}$,
P(X=3)=${C}_{5}^{3}(\frac{1}{4})^{3}(\frac{3}{4})^{2}$=$\frac{90}{1024}$,
P(X=4)=${C}_{5}^{4}(\frac{1}{4})^{4}(\frac{3}{4})$=$\frac{15}{1024}$,
P(X=5)=${C}_{5}^{5}(\frac{1}{4})^{5}$=$\frac{1}{1024}$,
所以随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{243}{1024}$ | $\frac{405}{1024}$ | $\frac{270}{1024}$ | $\frac{90}{1024}$ | $\frac{15}{1024}$ | $\frac{1}{1024}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<e<$\frac{1}{5}$ | B. | $\frac{1}{5}$<e<$\frac{1}{3}$ | C. | $\frac{1}{3}$<e<1 | D. | 0<e<$\frac{1}{5}$或$\frac{1}{3}$<e<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com