Question

3．已知等腰直角△ABC，AB=AC=4，点P，Q分别在边AB，BC上，$（\overrightarrow{PB}+\overrightarrow{BQ}）•\overrightarrow{BC}$=0，$\overrightarrow{PM}=2\overrightarrow{PQ}$，$\overrightarrow{AP}+\overrightarrow{AN}$=$\overrightarrow 0$，直线MN经过△ABC的重心，则|$\overrightarrow{AP}$|=（　　）

• A． $\frac{4}{3}$
• B． 2
• C． $\frac{8}{3}$
• D． 1

Answer 1

分析 可作出图形，根据条件便可得出PM⊥BC，Q为PM的中点，可设△ABC的重心为G，则由题意即可得到AG⊥BC，从而有AG∥PM，而由条件可以得到点A为PN的中点，并可求得$AG=\frac{2\sqrt{2}}{3}$，从而便可得到$PQ=\frac{2\sqrt{2}}{3}$，这样由△PBQ为等腰直角三角形即可求出PB的值，而AB=4，从而便可得出$|\overrightarrow{AP}|$的值．

解答 解：如图，设△ABC的重心为G，由条件知BC=$4\sqrt{2}$，△ABC为等腰直角三角形，∴$AG=\frac{2\sqrt{2}}{3}$；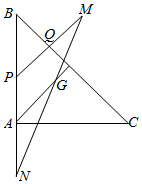

$（\overrightarrow{PB}+\overrightarrow{BQ}）•\overrightarrow{BC}=\overrightarrow{PQ}•\overrightarrow{BC}=0$；
∴PQ⊥BC，且$\overrightarrow{PM}=2\overrightarrow{PQ}$；
∴PM⊥BC，且Q为PM的中点；
又AG⊥BC；
∴AG∥PM；
由$\overrightarrow{AP}+\overrightarrow{AN}=\overrightarrow{0}$得，$\overrightarrow{AP}=-\overrightarrow{AN}$；
∴A为PN的中点；
∴PM=2AG；
∴$PQ=AG=\frac{2\sqrt{2}}{3}$；
△PBQ为等腰直角三角形，∠B=45°，∠PQB=90°；
∴$PB=\frac{\frac{2\sqrt{2}}{3}}{\frac{\sqrt{2}}{2}}=\frac{4}{3}$，AB=4；
∴$AP=4-\frac{4}{3}=\frac{8}{3}$；
即$|\overrightarrow{AP}|=\frac{8}{3}$．
故选：C．

点评 考查三角形重心的概念及重心的性质：重心到顶点距离是它到对边中点距离的2倍，向量加法及数乘的几何意义，向量垂直的充要条件，以及三角形中位线的性质，三角函数的定义．