
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() ⊥底面
⊥底面![]() ,若
,若![]() 分别为
分别为![]() 的中点.
的中点.
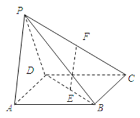
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() ⊥平面
⊥平面![]() .
.
【答案】(1)根据题意,证明线面平行,关键是先证明线线平行,即![]()
(2)对于面面垂直的证明,一般先证明线面垂直,![]() ,结合面面垂直的判定定理来得到。
,结合面面垂直的判定定理来得到。
【解析】
(Ⅰ)利用线面平行的判定定理,只需证明EF∥PA,即可.
(Ⅱ)先证明线面垂直,CD⊥平面PAD,再证明面面垂直,平面PAD⊥平面PDC即可.
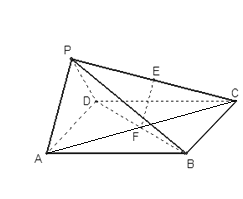
(Ⅰ)证明:连结AC,在正方形ABCD中,F为BD中点,正方形对角线互相平分,
∴F为AC中点,又E是PC中点,在△CPA中,EF∥PA,且PA平面PAD,
EF平面PAD, ∴EF∥平面PAD.
(Ⅱ)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,
![]() 平面
平面![]() ∴CD⊥平面PAD,∵CD平面PDC, ∴平面PAD⊥平面PDC
∴CD⊥平面PAD,∵CD平面PDC, ∴平面PAD⊥平面PDC


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() ,其前9项和为63.
,其前9项和为63.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行“交叉排列”,得到一个新的数列:
放在前面”的要求进行“交叉排列”,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有直线![]() 和平面
和平面![]() ,则下列四个命题中,正确的是( )
,则下列四个命题中,正确的是( )
A. 若m∥α,n∥α,则m∥nB. 若mα,nα,m∥β,l∥β,则α∥β
C. 若α⊥β,mα,则m⊥βD. 若α⊥β,m⊥β,mα,则m∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的中学生是否爱好运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 得,
得,![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是 ( )
A. 在犯错误的概率不超过0.001的前提下,认为“爱好运动与性别有关”
B. 在犯错误的概率不超过0.01的前提下,认为 “爱好运动与性别有关”
C. 在犯错误的概率不超过0.001的前提下,认为“爱好运动与性别无关”
D. 有![]() 以上的把握认为“爱好运动与性别无关”
以上的把握认为“爱好运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近日,某地普降暴雨,当地一大型提坝发生了渗水现象,当发现时已有![]() 的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为
的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为![]() 元,且渗水面积以每天
元,且渗水面积以每天![]() 的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积
的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积![]() ,该部门需支出服装补贴费为每人
,该部门需支出服装补贴费为每人![]() 元,劳务费及耗材费为每人每天
元,劳务费及耗材费为每人每天![]() 元.若安排
元.若安排![]() 名人员参与抢修,需要
名人员参与抢修,需要![]() 天完成抢修工作.
天完成抢修工作.
![]() 写出
写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() ,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
,不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分. 
(1)求椭圆C的方程;
(2)求△APB面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com