
分析 由题意知本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤$\frac{1}{2}$,0≤y≤$\frac{1}{2}$},做出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0≤x≤$\frac{1}{2}$,0≤y≤$\frac{1}{2}$,x-y≤$\frac{1}{4}$,y-x$≤\frac{1}{6}$},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果
解答 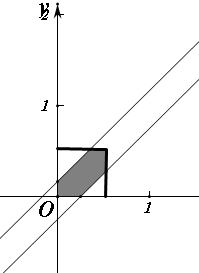 解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
设“丁香”和“小花”到达的时间分别为(8+x)时、(8+y)时,
则0≤x≤$\frac{1}{2}$,0≤y≤$\frac{1}{2}$,若两人见面,则x-y≤$\frac{15}{60}$=$\frac{1}{4}$,或者y-x$≤\frac{10}{60}=\frac{1}{6}$,
如图,正方形的面积为$\frac{1}{4}$,落在两直线之间部分的面积为$\frac{1}{4}-\frac{1}{18}-\frac{1}{32}$,
∴“丁香”和“小花”快乐地一起爬歌乐山的概率是$\frac{\frac{1}{4}-\frac{1}{18}-\frac{1}{32}}{\frac{1}{4}}=\frac{47}{72}$.
故答案为:$\frac{47}{72}$.
点评 本题是一个几何概型,解答此类问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{2}$-1,+∞) | B. | [$\sqrt{2}$,+∞) | C. | [2,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com