
【题目】已知函数f(x)=(x-k)ex,
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
【答案】(1)f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞);
(2)最小值为f(1)=(1-k)e
【解析】试题分析:(1)f′(x)=(x﹣k+1)ex,令f′(x)=0,得x=k﹣1.由此能求出f(x)的单调区间.
(2)当k﹣1≤0时,函数f(x)在区间[0,1]上递增,f(x)min=f(0)=﹣k;当1<k≤2时,函数f(x)在区间[0,k﹣1]上递减,(k﹣1,1]上递增,![]() ;当k>2时,函数f(x)在区间[0,1]上递减,f(x)min=f(1)=(1﹣k)e.
;当k>2时,函数f(x)在区间[0,1]上递减,f(x)min=f(1)=(1﹣k)e.
试题解析:
解:(1)f′(x)=(x-k+1)ex.
令f′(x)=0,得x=k-1.
当x变化时,f(x)与f′(x)的变化情况如下:
x | (-∞,k-1) | (k-1) | (k-1,+∞) |
f′(x) | - | 0 | + |
f(x) | -ek-1 |
所以,f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).
(2)当k-1≤0,即k≤1时,函数f(x)在[0,1]上单调递增,
所以f(x)在区间[0,1]上的最小值为f(0)=-k.
当0<k-1<1,即1<k<2时,
由(1)知f(x)在[0,k-1)上单调递减,在(k-1,1]上单调递增,所以f(x)在区间[0,1]上的最小值为
f(k-1)=-ek-1.
当k-1≥1,即k≥2时,函数f(x)在[0,1]上单调递减,
所以f(x)在区间[0,1]上的最小值为f(1)=(1-k)e.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).
).
(Ⅰ)把曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(Ⅱ)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,下顶点为
,下顶点为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, ![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且三角形
,且三角形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相切,过焦点
相切,过焦点![]() ,
, ![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
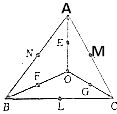
【题目】平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 
(1)试用 ![]() ,
, ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() ,
, ![]() ;
;
(2)证明:线段EL,FM,GN交于一点且互相平分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内的动点P到定直线l:x=![]() 的距离与点P到定点F(
的距离与点P到定点F(![]() ,0)之比为
,0)之比为![]() .
.
(1)求动点P的轨迹C的方程;
(2)若点N为轨迹C上任意一点(不在x轴上),过原点O作直线AB,交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为k1、k2,问k1·k2是否为定值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com