
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,通项
,通项![]() 满足
满足![]() (
(![]() 是常数,
是常数, ![]() 且
且![]() ).
).
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)当![]() 时,证明
时,证明![]() ;
;
(Ⅲ)设函数![]() ,
, ![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 对
对![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)对
;(2)见解析;(3)对![]() 都成立的正整数
都成立的正整数![]() 存在,其值为1,2,3.
存在,其值为1,2,3.
【解析】试题分析:(1)先根据和项与通项关系得项递推关系,再根据等比数列定义以及通项公式求数列![]() 的通项公式;(2)根据等比数列前n项和公式得
的通项公式;(2)根据等比数列前n项和公式得![]() ,再证结论(3)先根据对数运算法则化简
,再证结论(3)先根据对数运算法则化简![]() ,再利用裂项相消法求和:
,再利用裂项相消法求和: ![]() ,根据数列单调性确定
,根据数列单调性确定![]() 最小值为2,即得
最小值为2,即得![]() ,所以
,所以![]() 的值为1,2,3
的值为1,2,3
试题解析:(Ⅰ)由题意![]() ,得
,得![]() 所以
所以![]()
当![]() 时,
时, ![]() ,所以
,所以![]()
故数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列
的等比数列
所以![]()
(Ⅱ)由(Ⅰ)知,当![]() 时,
时, ![]()
所以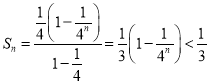
(Ⅲ)因为![]()
所以![]()
![]()
![]()
![]()
![]()
所以![]()
所以![]()
欲使![]() ,即
,即![]() 对
对![]() 都成立
都成立
须有![]()
而当![]() 时,
时, ![]() 随
随![]() 的增大而增大
的增大而增大
所以![]()
又![]() 为正整数,所以
为正整数,所以![]() 的值为1,2,3
的值为1,2,3
故使![]() 对
对![]() 都成立的正整数
都成立的正整数![]() 存在,其值为1,2,3.
存在,其值为1,2,3.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点
的左焦点![]() 和上顶点
和上顶点![]() 在直线
在直线![]() 上,
上, ![]() 为椭圆上位于
为椭圆上位于![]() 轴上方的一点且
轴上方的一点且![]() 轴,
轴, ![]() 为椭圆
为椭圆![]() 上不同于
上不同于![]() 的两点,且
的两点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,三个函数的定义域均为集合
,三个函数的定义域均为集合![]() .
.
(1)若![]() 恒成立,满足条件的实数
恒成立,满足条件的实数![]() 组成的集合为
组成的集合为![]() ,试判断集合
,试判断集合![]() 与
与![]() 的关系,并说明理由;
的关系,并说明理由;
(2)记 ,是否存在
,是否存在![]() ,使得对任意的实数
,使得对任意的实数![]() ,函数
,函数![]() 有且仅有两个零点?若存在,求出满足条件的最小正整数
有且仅有两个零点?若存在,求出满足条件的最小正整数![]() ;若不存在,说明理由.(以下数据供参考:
;若不存在,说明理由.(以下数据供参考: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示,受“闺蜜门”时间影响,韩国总统朴槿惠的民意支持率持续下跌,在所调查的1000个对象中,年龄在[20,30)的群体有200人,支持率为0%,年龄在[30,40)和[40,50)的群体中,支持率均为3%;年龄在[50,60)和[60,70)的群体中,支持率分别为6%和13%,若在调查的对象中,除[20,30)的群体外,其余各年龄层的人数分布情况如频率分布直方图所示,其中最后三组的频数构成公差为100的等差数列.
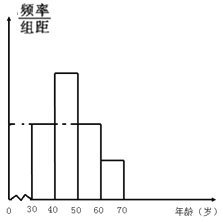
(1)依频率分布直方图求出图中各年龄层的人数
(2)请依上述支持率完成下表:
年龄分布 是否支持 | [30,40)和[40,50) | [50,60)和[60,70) | 合计 |
支持 | |||
不支持 | |||
合计 |
根据表中的数据,能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关?
附表:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() 参考数据:125×33=15×275,125×97=25×485)
参考数据:125×33=15×275,125×97=25×485)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
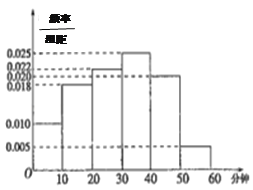
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的2×2列联表,若按95%的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)现在从该地区非体育迷的电视观众中,采用分层抽样方法选取5名观众,求从这5名观众选取两人进行访谈,被抽取的2名观众中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
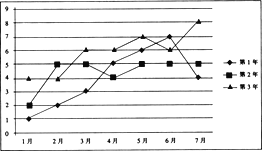
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 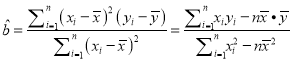 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com