
已知向量m=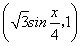 ,n=
,n=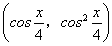 .
.
(1)若m·n=1,求cos 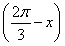 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
(1)-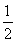 (2)
(2)
【解析】(1)m·n=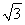 sin
sin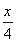 cos
cos +cos2
+cos2 =
=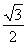 sin
sin 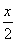 +
+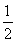 cos
cos 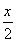 +
+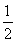 =sin
=sin 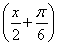 +
+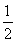 .(3分)
.(3分)
因为m·n=1,所以sin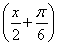 =
=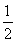 ,
,
故cos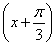 =1-2sin2
=1-2sin2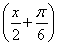 =
=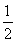 ,
,
所以cos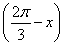 =-cos
=-cos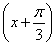 =-
=-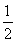 .(6分)
.(6分)
(2)因为(2a-c)cos B=bcos C,
由正弦定理得(2sin A-sin C)cos B=sin Bcos C,
即2sin Acos B-sin Ccos B=sin Bcos C,
所以2sin Acos B=sin(B+C),(8分)
又因为A+B+C=π,
所以sin(B+C)=sin A,且sin A≠0,
所以cos B=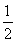 ,B=
,B= ,0<A<
,0<A<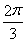 ,
,
所以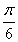 <
<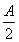 +
+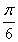 <
<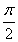 ,
,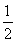 <sin
<sin <1,(12分)
<1,(12分)
又f(x)=m·n=sin +
+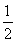 ,
,
所以f(A)=sin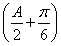 +
+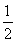 ∈
∈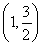 ,
,
故函数f(A)的取值范围是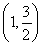 .(14分)
.(14分)


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:解答题
已知在递增等差数列{an}中,a1=2,a1,a3,a7成等比数列,{bn}的前n项和为Sn,且Sn=2n+1-2.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=abn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:解答题
已知函数f(x)=ln x+ -1.
-1.
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
命题“若a2+b2=0,则a=0且b=0”的逆否命题是( )
A.若a2+b2≠0,则a≠0且b≠0 B.若a2+b2≠0,则a≠0或b≠0
C.若a=0且b=0,则a2+b2≠0 D.若a≠0或b≠0,则a2+b2≠0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-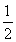 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
如图,在四棱锥P ?ABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
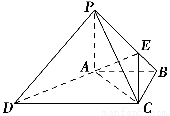
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,且c=2,C=60°.
(1)求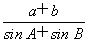 的值;
的值;
(2)若a+b=ab,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练E组练习卷(解析版) 题型:填空题
曲线y= 在点(-1,-1)处的切线方程为________.
在点(-1,-1)处的切线方程为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练B组练习卷(解析版) 题型:填空题
定义集合M、N的新运算如下:Mx N={x|x∈M或x∈N,但x∉M∩N},若集合M={0,2,4,6,8,10},N={0,3,6,9,12,15},则(Mx N)xM等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com