练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝ln x＋－1.

    (1)求函数f(x)的单调区间；

    (2)设m∈R，对任意的a∈(－1,1)，总存在x0∈[1，e]，使得不等式ma－f(x0)＜0成立，求实数m的取值范围．

     

    （1）单调递增区间是(1，＋∞)．单调递减区间是(0,1)．（2）

    【解析】(1)f′(x)＝－＝，x＞0.

    令f′(x)＞0，得x＞1，因此函数f(x)的单调递增区间是(1，＋∞)．

    令f′(x)＜0，得0＜x＜1，因此函数f(x)的单调递减区间是(0,1)．

    (2)依题意，ma＜f(x)max.

    由(1)知，f(x)在x∈[1，e]上是增函数，

    ∴f(x)max＝f(e)＝ln e＋－1＝.

    ∴ma＜，即ma－＜0对于任意的a∈(－1,1)恒成立．

    ∴解得－≤m≤.

    ∴m的取值范围是.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷5练习卷（解析版） 题型：选择题

    已知抛物线y2＝2px(p＞0)与双曲线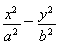＝1(a＞0，b＞0)的一条渐近线交于一点M(1，m)，点M到抛物线焦点的距离为3，则双曲线的离心率等于(　　)

    A．3 B．4 C.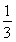 D.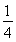

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷3练习卷（解析版） 题型：选择题

    设等差数列{an}的前n项和为Sn，若Sm－1＝－2，Sm＝0，Sm＋1＝3，则m＝(　　)

    A．3 B．4 C．5 D．6

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷2练习卷（解析版） 题型：选择题

    据市场调查，某种商品一年中12个月的价格与月份的关系可以近似地用函数f(x)＝Asin(ωx＋φ)＋7(A＞0，ω＞0，|φ|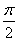＜)来表示(x为月份)，已知3月份达到最高价9万元，7月份价格最低，为5万元，则国庆节期间的价格约为(　　)

    A．4.2万元 B．5.6万元

    C．7万元 D．8.4万元

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷2练习卷（解析版） 题型：选择题

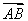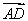    在梯形ABCD中，AB∥CD，且|AB|＝λ|DC|，设＝a，＝b，则＝(　　)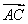

    A．λa＋b B．a＋λb

    C.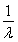a＋b D．a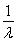＋b

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：填空题

    设函数f(x)＝ax＋b(0≤x≤1)，则a＋2b＞0是f(x)＞0在[0,1]上恒成立的________条件．(填充分但不必要，必要但不充分，充要，既不充分也不必要)

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年（安徽专用）高考数学（文）专题阶段评估模拟卷1练习卷（解析版） 题型：选择题

    设z＝x＋y，其中实数x，y满足若z的最大值为6，则z的最小值为(　　)

    A．－3 B．－2

    C．－1 D．0

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练解答题押题练C组练习卷（解析版） 题型：解答题

    已知向量m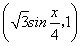＝，n＝.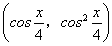

    (1)若m·n＝1，求cos 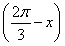的值；

    (2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cos B＝bcos C，求函数f(A)的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学（文）三轮专题体系通关训练填空题押题练D组练习卷（解析版） 题型：填空题

    已知函数f(x)＝－xln x＋ax在(0，e)上是增函数，函数g(x)＝|ex－a|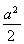＋，当x∈[0，ln 3]时，函数g(x)的最大值M与最小值m的差为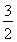，则a＝________.

     

    查看答案和解析>>

    同步练习册答案