
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(3)证明:![]()
![]() .
.
【答案】(1)![]() 上增函数,
上增函数,![]() 增,
增,![]() 减;(2)证明见解析
减;(2)证明见解析
【解析】试题分析:(1)求出函数的导数,计算![]() 的值,得到关于k的方程,解出即可;(2)判断
的值,得到关于k的方程,解出即可;(2)判断![]() 时,
时,![]() 在
在![]() 上是增函数,而
上是增函数,而![]() 不成立,故
不成立,故![]() ,又由(1)知
,又由(1)知![]() 的最大值为
的最大值为![]() ,由此能确定实数
,由此能确定实数![]() 的取值范围.(3)由(2)知,当k=1时,有
的取值范围.(3)由(2)知,当k=1时,有![]() 在
在![]() 恒成立,且
恒成立,且![]() 在
在![]() 上是减函数,
上是减函数,![]() ,即
,即![]() 在
在![]() 上恒成立,由此能够证明不等式成立即可.
上恒成立,由此能够证明不等式成立即可.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,若
时,若![]() ,则
,则![]() ;若
;若![]() ,
,
则![]() .所以
.所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(Ⅱ)由(Ⅰ)知![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
而![]() 不成立,故
不成立,故![]() ,
,
当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]()
![]() .要使
.要使![]() 恒成立,则
恒成立,则![]() 即可.
即可.
故![]() ,解得
,解得![]() .
.
(Ⅲ)由(Ⅱ)知,当![]() 时有
时有![]() 在
在![]() 恒成立,且
恒成立,且![]() 在
在![]() 上是减函数,
上是减函数,![]() ,所以
,所以![]() 在
在![]() 上恒成立.令
上恒成立.令![]() ,则
,则![]() ,即
,即![]() ,从而
,从而![]() ,
,
所以![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 依逆时针次序排列,点
依逆时针次序排列,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(2)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
:![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上不同的三点,并且
上不同的三点,并且![]() 为
为![]() 的重心,试探究
的重心,试探究![]() 的面积是否为定值.若是,求出这个定值;若不是,请说明理由.
的面积是否为定值.若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
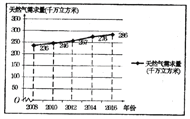
【题目】2017年12月,针对国内天然气供应紧张的问题,某市政府及时安排部署,加气站采取了紧急限气措施,全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况,对该地区某些年份天然气需求量进行了统计,并绘制了相应的折线图.
(Ⅰ)由折线图可以看出,可用线性回归模型拟合年度天然气需示量![]() (单位:千万立方米)与年份
(单位:千万立方米)与年份![]() (单位:年)之间的关系.并且已知
(单位:年)之间的关系.并且已知![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,试确定
,试确定![]() 的值,并预测2018年该地区的天然气需求量;
的值,并预测2018年该地区的天然气需求量;
(Ⅱ)政府部门为节约能源出台了《购置新能源汽车补贴方案》,该方案对新能源汽车的续航里程做出了严格规定,根据续航里程的不同,将补贴金额划分为三类,A类:每车补贴1万元,B类:每车补贴2.5万元,C类:每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计,结果如下表:
类型 |
|
|
|
车辆数目 | 10 | 20 | 30 |
为了制定更合理的补贴方案,政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况,在该出租车公司的60辆车中抽取6辆车作为样本,再从6辆车中抽取2辆车进一步跟踪调查.若抽取的2辆车享受的补贴金额之和记为“![]() ”,求
”,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数.
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6.在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]()
![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某班的50名学生进行不记名问卷调查,内容为本周使用手机的时间长,如表:
时间长(小时) |
|
|
|
|
|
女生人数 | 4 | 11 | 3 | 2 | 0 |
男生人数 | 3 | 17 | 6 | 3 | 1 |
(1)求这50名学生本周使用手机的平均时间长;
(2)时间长为![]() 的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
的7名同学中,从中抽取两名,求其中恰有一个女生的概率;
(3)若时间长为![]() 被认定“不依赖手机”,
被认定“不依赖手机”,![]() 被认定“依赖手机”,根据以上数据完成
被认定“依赖手机”,根据以上数据完成![]() 列联表:
列联表:
不依赖手机 | 依赖手机 | 总计 | |
女生 | |||
男生 | |||
总计 |
能否在犯错概率不超过0.15的前提下,认为学生的性别与依赖手机有关系?
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,离心率
,离心率![]() ,
, ![]() 为坐标原点,圆
为坐标原点,圆![]() 与直线
与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知四边形![]() 内接于椭圆
内接于椭圆![]() .记直线
.记直线![]() 的斜率分别为
的斜率分别为![]() ,试问
,试问![]() 是否为定值?证明你的结论.
是否为定值?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com