
【题目】已知函数![]() .
.
(1)试判断f (x)的单调性,并证明你的结论;
(2)若f (x)为定义域上的奇函数,求函数f (x)的值域.
【答案】(1)增函数,证明见解析;(2)![]() .
.
【解析】
(1)f (x)是增函数,利用单调性的定义进行证明;
(2)用奇函数的性质先求出a,再求函数f (x)的值域.
(1)f (x)是增函数.
证明如下:函数f (x)的定义域为(﹣∞,+∞),且![]()
任取x1,x2∈(﹣∞,+∞),且x1<x2,
则![]() .
.
因为y=2x在R上单调递增,且x1<x2,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以f(x2)﹣f(x1)>0,即f(x2)>f(x1),
所以f(x)在(﹣∞,+∞)上是单调增函数.
(2)因为f(x)是定义域上的奇函数,所以f(﹣x)=﹣f(x),
即![]() 对任意实数x恒成立,化简得
对任意实数x恒成立,化简得![]() ,
,
所以2a﹣2=0,即a=1.所以![]() ,
,
因为2x+1>1,所以![]() ,可得
,可得![]() ,则
,则![]() .
.
故函数f (x)的值域为(﹣1,1).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,动点M到点F(1,0)的距离与它到直线x=2的距离之比为 ![]() .
.
(1)求动点M的轨迹E的方程;
(2)设直线y=kx+m(m≠0)与曲线E交于A,B两点,与x轴、y轴分别交于C,D两点(且C,D在A,B之间或同时在A,B之外).问:是否存在定值k,对于满足条件的任意实数m,都有△OAC的面积与△OBD的面积相等,若存在,求k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为定义域
是否为定义域![]() 上的“局部奇函数”?若是,求出所有满足
上的“局部奇函数”?若是,求出所有满足![]() 的
的![]() 的值;若不是,请说明事由.
的值;若不是,请说明事由.
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
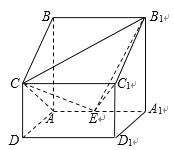
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长度;
的长度;
(Ⅲ)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?(结论不要求证明)
?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为{x|x≠0}的函数f(x)满足:f(xy)=f(x)f(y),f(x)>0且在区间(0,+∞)上单调递增,若m满足f(log3m)+f( ![]() )≤2f(1),则实数m的取值范围是( )
)≤2f(1),则实数m的取值范围是( )
A.[ ![]() ,1)∪(1,3]
,1)∪(1,3]
B.[0, ![]() )∪(1,3]
)∪(1,3]
C.(0, ![]() ]
]
D.[1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某商场旅游鞋的日销售情况,现抽取部分顾客购鞋的尺码,将所得数据绘成如图所示频率分布直方图,已知图中从左到右前三组的频率之比为1:2:3,第二组的频数为10. 
(1)用频率估计概率,求尺码落在区间(37.5,43.5]概率约是多少?
(2)从尺码落在区间(37.5,39.5](43.5,45.5]顾客中任意选取两人,记在区间(43.5,45.5]的人数为X,求X的分布列及数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M. 
(1)求证:O、B、D、E四点共圆;
(2)求证:2DE2=DMAC+DMAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(百分制)如表所示:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若数学成绩90分(含90分)以上为优秀,物理成绩85(含85分)以上为优秀.有多少把握认为学生的数学成绩与物理成绩之间有关系( )
A.99.5%
B.99.9%
C.97.5%
D.95%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com