
| A. | ②④ | B. | ②③ | C. | ①③ | D. | ①④ |
分析 分别令x=1、x=0求出二项式(x-1)2005所有项的系数和与常数项,判定①正确;
根据二项式展开式的通项公式求出第六项,判定②错误;
根据二项展开式的特点可知系数绝对值最大的项,判定③错误;
当x=2006时,(x-1)2005除以2006的余数是2006-l,判定④正确.
解答 解:在二项式(x-1)2005中,令x=1得二项式(x-1)2005所有项的系数和为0,
令x=0得常数项为-l,∴非常数项的系数和是1,①正确;
二项展开式的第六项为T5+1=${C}_{2005}^{5}$•x2000•(-1)5=-C20055x2000,∴②错误;
二项展开式中系数绝对值最大的为${C}_{2005}^{\frac{2005-1}{2}}$=C20051002,
和-${C}_{2005}^{\frac{2005+1}{2}}$=-C20051003,
得系数最大的项是第1003项C20051002•x1003,∴③错误;
当x=2006时,(x-1)2005除以2 006的余数是2006-l=2005,∴④正确.
综上,以上正确命题的序号是①④.
故选:D.
点评 本题主要考查了二项式系数的性质,展开式的特定项以及系数最大项问题,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 20π | D. | 5π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
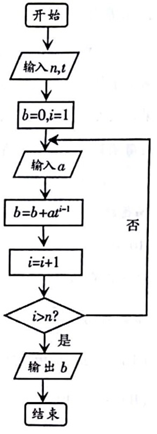 在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )| A. | 179 | B. | 178 | C. | 147 | D. | 146 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 16π | D. | 9π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com