
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:| 年龄(岁) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | m | n | 14 | 12 | 8 | 6 |
| 知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
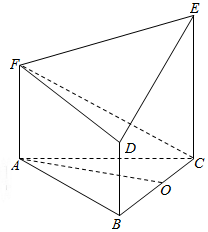
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com