
分析 (1)由a=1,得出f(x)的解析式,求切线方程,即先求f′(x)在x=0出的值为切线的斜率.由点斜式求出切线方程即可.
(2)求出导函数,并讨论其等价函数h(x),从△>0,△=0,△<0三种情况讨论.
(3)利用导数证明不等式:构造辅助函数,把不等式的证明转化为利用导函数研究函数单调性或最值,从而证明不等式.
解答 解:(1)当a=-1时,f(x)=x2-ln(x+1)
f′(x)=2x-$\frac{1}{x+1}$=$\frac{2{x}^{2}+2x-1}{x+1}$=$\frac{2(x+\frac{1}{2})^{2}-\frac{3}{2}}{x+1}$
f′(0)=-1
即切线方程的斜率是-1
∴切线方程为y=-x
(2)∵函数f(x)=x2+aln(x+1),其中a≠0
∴f(x)的定义域为(0,+∞)
f′(x)=2x+$\frac{a}{x+1}$=$\frac{2{x}^{2}+2x+a}{x+1}$
令h(x)=2x2+2x+a=2(x+$\frac{1}{2}$)2+a-$\frac{1}{2}$
①a<$\frac{1}{2}$,且a≠0时,△>0,h(x)=0有两个根,x1=$\frac{-1-\sqrt{1-2a}}{2}$,x2=$\frac{-1+\sqrt{1-2a}}{2}$
当0<a<$\frac{1}{2}$时,x1∈(-1,-$\frac{1}{2}$),x2∈(-$\frac{1}{2}$,+∞),此时f(x)有2个极值点.
当a<0时,x1∈(-∞,-1),x2∈(-$\frac{1}{2}$,+∞),此时f(x)有1个极值点.
②a=$\frac{1}{2}$时,△=0,
∴h(x)≥0,
则f(x)≥0,
∴f(x)在(-1,+∞)上为增函数
∴f(x)无极值点
③a>$\frac{1}{2}$时,△<0,
∴h(x)>0,则f(x)>0,
∴f(x)在[-1,+∞)上为增函数,
∴f(x)无极值点.
综上,当a≥$\frac{1}{2}$时,无极值点;当0<a<$\frac{1}{2}$时,有2个极值点;当a<0时,有1个极值点.
(3)当a=-1时,函数f(x)=x2-ln(x+1),
令函数g(x)=x3-f(x)=x3-x2+ln(x+1)
则g′(x)=3x2-2x+$\frac{1}{x+1}$=$\frac{3{x}^{3}+(x-1)^{2}}{x+1}$
当x∈[0,+∞)时,g′(x)>0
∴函数g(x)在[0,+∞)上单调递增,
又∵g(0)=0
∴x∈(0,+∞)时,恒有g(x)>g(0)=0
即x2<x3+ln(x+1)恒成立
取x=$\frac{1}{n+1}$ 则有ln(1+$\frac{1}{n+1}$)>$\frac{1}{(n+1)^{2}}$-$\frac{1}{(n+1)^{3}}$恒成立
即不等式ln($\frac{n+2}{n+1}$)>$\frac{n}{(n+1)^{3}}$恒成立
点评 本题考查函数与导函数的关系.在导函数的应用中可以通过构造等价函数来研究.尤其是(3)中将导函数与不等式建立关系.属于偏难题型.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
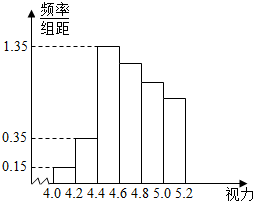 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 26 | B. | 49 | C. | 52 | D. | 98 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com