
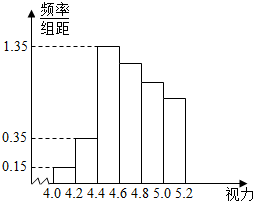
 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (1)设各组的频率为fi(i=1,2,3,4,5,6),由已知得后四组频数依次为27,24,21,18,由此能求出估计全年级视力在5.0以下的人数.
(2)求出K2,由此能求出在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.
(Ⅲ)依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,X可取0、1、2、3,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
解答 解:(1)设各组的频率为fi(i=1,2,3,4,5,6),
由图可知,第一组有3人,第二组7人,第三组27人,…(1分)
因为后四组的频数成等差数列,
所以后四组频数依次为27,24,21,18…(2分)
所以视力在5.0以下的频率为:$\frac{3+7+27+24+21}{100}$=0.82,
故全年级视力在5.0以下的人数约为$1000×\frac{82}{100}=820$…(3分)
(2)${k^2}=\frac{{100×{{(41×18-32×9)}^2}}}{50×50×73×27}=\frac{300}{73}≈4.110>3.841$
因此在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.…(6分)
(Ⅲ)依题意9人中年级名次在1~50名和951~1000名分别有3人和6人,X可取0、1、2、3,…(7分)
$P(X=0)=\frac{C_6^3}{C_9^3}=\frac{20}{84}$,
$P(X=1)=\frac{C_6^2C_3^1}{C_9^3}=\frac{45}{84}$,
$P(X=2)=\frac{C_6^1C_3^2}{C_9^3}=\frac{18}{84}$,
$P(X=3)=\frac{C_3^3}{C_9^3}=\frac{1}{84}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{20}{84}$ | $\frac{45}{84}$ | $\frac{18}{84}$ | $\frac{1}{84}$ |
点评 本题考查频率分布直方图的应用,考查离散型机随机变量概率分布列、数学期望的求法,是中档题,解题时要认真审题,注意排列组合的合理运用.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
 某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:
某校举行一次安全知识教育检查活动,从全校1500名学生中随机抽取50名参加笔试,测试成绩的频率分布表如下:| 分组(分数段) | 频数(人数) | 频率 |
| [50,60) | a | 0.08 |
| [60,70) | 13 | 0.26 |
| [70,80) | 16 | 0.32 |
| [80,90) | 10 | 0.20 |
| [90,100) | b | c |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | v(t)=-4t+8 | B. | v(t)=4t-8 | C. | v(t)=-8t+2 | D. | v(t)=8t-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 80 | C. | -16或32 | D. | -64或80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
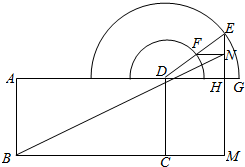 如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.
如图所示,长方形ABCD中,AB=2,BC=4,以D为圆心的两个圆心半圆,半径分别为1和2,G为大半圆直径的右端点,E为大半圆上的一个动点,DE与小半圆交于点F,EM⊥BC,垂足为M,EM与大半圆直径交于点H,FN⊥EM,垂足为N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com